Если
взять ![]() , то получим
, то получим ![]() .
Скорость света обладает свойством инвариантности.
.
Скорость света обладает свойством инвариантности.
Формула
(12.3) упрощается, если ввести в рассмотрение новые функции ![]()
![]()
![]() и
и
![]() (гиперболические тангенсы скоростей):
(гиперболические тангенсы скоростей):
![]() ,
, ![]() .
.
Соотношение (12.3) принимает вид
![]() ,
,
т.е.
при параллельном движении частицы и системы отсчета ![]() складываются
гиперболические тангенсы скоростей. Использование преобразования Лоренца
предполагает, что относительная скорость систем отсчета, т.е относительная
скорость материальных объектов не может быть больше
складываются
гиперболические тангенсы скоростей. Использование преобразования Лоренца
предполагает, что относительная скорость систем отсчета, т.е относительная
скорость материальных объектов не может быть больше ![]() , так
как при
, так
как при ![]() преобразование становится мнимым. Можно
убедиться, что при произвольном движении частицы справедлива формула
преобразование становится мнимым. Можно
убедиться, что при произвольном движении частицы справедлива формула
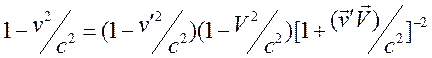 .
.
Отсюда
следует, что при произвольном движении частицы справедливо утверждение: если ![]() , то и
, то и ![]() .
Скорость частиц не превосходит скорости света. Если же
.
Скорость частиц не превосходит скорости света. Если же ![]() ,
то и
,
то и ![]() .
.
Определим,
как изменяется направление скорости частицы при переходе из одной инерциальной
системы в другую. Ограничимся случаем, когда траектория движения частицы лежит
в плоскости ![]() .Обозначим через
.Обозначим через ![]() угол
между
угол
между ![]()
и
осью ![]() . (напомним, что
. (напомним, что 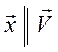 ),
тогда
),
тогда
![]()
![]()
из формул преобразования скоростей получается
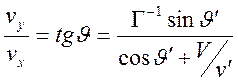 .
.
В
случае ![]() получаем формулу для аберрации света (аберрация
– латинское слово, означающее уклонение, заблуждение; в данном разделе
подразумевается изменение направления распространения света при переходе из
одной системы отсчета в другую)
получаем формулу для аберрации света (аберрация
– латинское слово, означающее уклонение, заблуждение; в данном разделе
подразумевается изменение направления распространения света при переходе из
одной системы отсчета в другую)
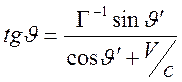 .
.
При
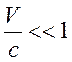 имеем
имеем
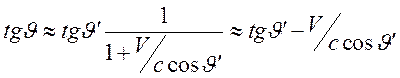
или
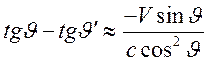 .
.
При
малых значениях ![]() будет
будет ![]() ,
,
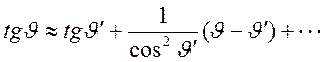 и формула для аберрации света приводится к
виду
и формула для аберрации света приводится к
виду
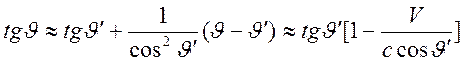
и
окончательно имеем описание малого изменения направления света при ![]() :
:
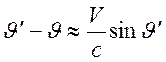 .
.
12.4. Релятивистская механика частицы. 4 – скорость. 4 – ускорение. Четырехмерное уравнение движения. 4 – импульс. Сила Минковского. Энергия частицы. Принцип эквивалентности.
1. В
классической механике импульс частицы определяется как ![]() ,
где
,
где ![]() - масса частицы,
- масса частицы, ![]() -
ее скорость. Такое определение не может быть правильным в теории
относительности при требовании использования преобразования Лоренца. Дело в
следующем: импульс может быть сколь угодно большим как в классической, так и в
релятивистской механике, скорость же в теории относительности ограничена сверху
величиной
-
ее скорость. Такое определение не может быть правильным в теории
относительности при требовании использования преобразования Лоренца. Дело в
следующем: импульс может быть сколь угодно большим как в классической, так и в
релятивистской механике, скорость же в теории относительности ограничена сверху
величиной ![]() .Поэтому определение
.Поэтому определение ![]() должно быть изменено.
должно быть изменено.
Все физические величины могут быть объединены в совокупности, которые являются либо скалярами, либо 4 – векторами, либо ; 4- тензорами, либо спинорами (квадратичные комбинации спиноров образуют 4 - векторы). В математике доказано, что иных объектов, связанных с преобразованиями Лоренца не существует. Установив, вектором или тензором является некоторая величина, мы получаем возможность классифицирования всех физических величин. Так как все инерциальные системы отсчета эквивалентны, то все законы природы должны выглядеть одинаково в этих системах. Введя понятие 4 – вектора, либо 4 – тензора, следует каждому закону природы придать четырехмерную формулировку, она и будет инвариантной относительно преобразований Лоренца.
Релятивистская механика описывается в четырехмерном
пространстве Минковского. При определении четырехмерных векторов (4 - векторов)
скорости и ускорения за основу принимается 4 – вектор ![]() ,
записываемый в одной из двух форм (ковариантной или контравариантной):
,
записываемый в одной из двух форм (ковариантной или контравариантной):
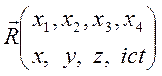 ,
, 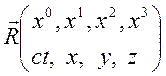 .
.
4
– скорость можно определить отношением 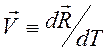 , где
, где ![]() должен быть скаляром (все скаляры являются
инвариантами для преобразования Лоренца). В качестве
должен быть скаляром (все скаляры являются
инвариантами для преобразования Лоренца). В качестве ![]() естественно
взять некоторое «выделенное» время. Таким временем является собственное
время частицы, определяемое однозначно через интервал
естественно
взять некоторое «выделенное» время. Таким временем является собственное
время частицы, определяемое однозначно через интервал
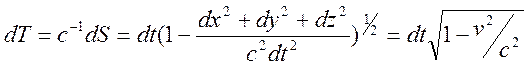 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.