Специальная теория относительности. Преобразования Лоренца. Промежуток времени между событиями. Длина отрезка. Лоренцово сокращение. Четырехмерное пространство Минковского. Интервал. Собственное время. Сложение скоростей, страница 6

12.5. Движение заряженной частицы во внешнем  постоянном электромагнитном поле в вакууме. Циклотронная частота.

            Сначала исследуем следующую ситуацию.

1). На частицу с зарядом  действует трехмерная сила

                                                , 

где  - скорость частицы. Трехмерное уравнение движения имеет вид

                                    .

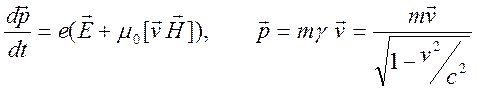Следует отметить, что это нелинейное уравнение. Изменение энергии частицы во времени описывается соотношением (это четвертое уравнение движения)

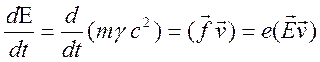                                    ,                  (12.9)

изменение энергии частицы определяется только электрическим полем, так как магнитная сила перпендикулярна скорости, и она не производит работы.

Сравнивая формулы для трехмерного импульса и для энергии

                        ,                 ,

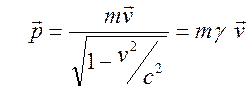получаем связь импульса и энергии . Подстановка этого выражения в уравнение движения и учет (12.9) позволяет найти релятивистское ускорение частицы как нелинейную функцию скорости частицы

                                    .

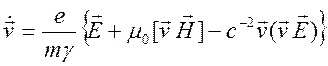Учет релятивистских эффектов в формуле для ускорения дает два отличия от описания классической механики: во – первых появляется характерный множитель 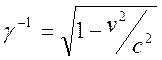, а во – вторых, возникает добавочный член с напряженностью электрического поля .

            2). Рассмотрим частный случай . Найдем закономерность эволюции  и определим траекторию частицы. Введем систему координат следующим образом: 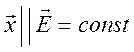, , где . Тогда из уравнения движения

                                               

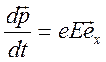
Получим

                                                ,

значит, имеет место описание эволюции компонент вектора

                                                .

Начало отсчета времени выберем так, чтобы . Полученные соотношения представляют со бой нелинейные уравнения относительно вектора скорости.

            Примем во внимание соотношения

            ,            ,

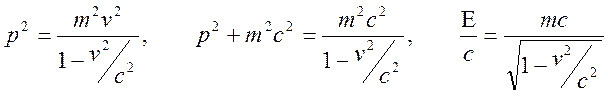Получим описание изменения энергии во времени

                                    .

Учитывая соотношения , получим представление для вектора скорости как функции времени 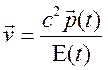. Компоненты вектора скорости заряженной частицы, находящейся во внешнем электрическом поле имеют вид

                        ,                 .

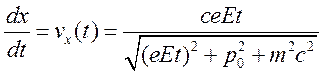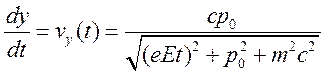При неограниченном возрастании времени проекция скорости вдоль поля стремится к скорости света , а перпендикулярная проекция скорости стремится к нулю. Учитывая, что  и 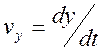, можно определить траекторию частицы. Можно показать, что она имеет вид параболы

                                               

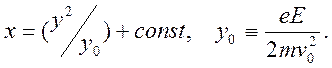
            3). Исследуем теперь движение частицы в постоянном магнитном поле при отсутствии электрического поля. Последнее обстоятельство (см. пункт 1).) приводит к сохранению энергии

                                    ,         .

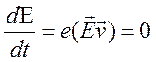Трехмерное уравнение движения линейно, и имеет вид

                                    .

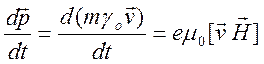Получаем формулу для ускорения

                                                ,

где угловая скорость 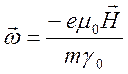 называется циклотронной частотой (частотой гирорезонанса заряженной частицы). В нерелятивистской ситуации 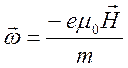. Вектор скорости представим в виде суммы , где  - компонента вдоль направления вектора  Индексом  отмечена компонента вектора, перпендикулярная . Движение в плоскости , перпендикулярной  происходит по окружности:

            .,  ,            .

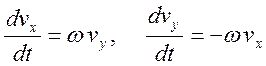Радиус этой окружности дается формулой

                                                ,

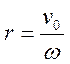так как .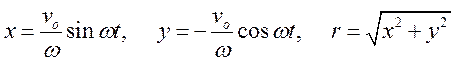

Составляющая скорости частицы вдоль  не изменяется, поэтому траектория частицы это винтовая линия с осью, направленной вдоль , и с радиусом .