Специальная теория относительности. Преобразования Лоренца. Промежуток времени между событиями. Длина отрезка. Лоренцово сокращение. Четырехмерное пространство Минковского. Интервал. Собственное время. Сложение скоростей, страница 2

            Получим преобразование Лоренца, соответствующее трехмерному движению системы  в произвольном направлении с постоянной скоростью , 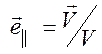. Вектор  представим в виде составляющей поперек направления вектора скорости и  - составляющей вдоль этого направления

                                                ,

где 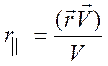. Так как поперечная составляющая вектора скорости 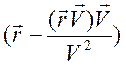имеет нулевую составляющую, то не происходит изменения ее при переходе от одной инерциальной системы  к другой . Преобразование Лоренца имеет вид

                                                ,

                                                ,         ,

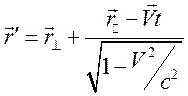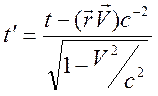            Преобразования Лоренца и введение относительности понятия времени составляют основу специальной теории относительности. Эта теория была создана Эйнштейном (1905 г.), значительный вклад был сделан Лоренцом и Пуанкаре.

12.2. Интервал. Собственное время. Если рассматриваются два события  и  в одной системе отсчета, то согласно преобразованию Лоренца инвариантом будет величина

                        ,

называемая интервалом между рассматриваемыми событиями:

                                                .

Иногда понятие интервал вводится иначе

                       

Для бесконечно близких событий в системе  и в системе интервалы определяются соотношениями

                                    ,

                                    .

Аналогичные определения вводятся и для интервала .

Пусть часы расположены в системе  и в этой системе они неподвижны. Эта система пусть движется произвольным образом относительно системы  (система  не является инерциальной). Однако в течении бесконечно малых промежутков времени систему  можно считать инерциальной (имеет место локальная инерциальность). Относительно системы  часы покоятся, значит . Возьмем бесконечно малый промежуток времени  в системе  и найдем соответствующий ему промежуток времени  в системе . Из условия инвариантности интервала будем иметь

                                    ,

                                   

где ,    - скорость перемещения часов и системы  относительно системы . В результате получим связь промежутков времени в двух системах:

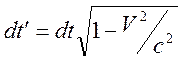                                    ,     - произвольная функция времени. Система  является локально инерциальной (инерциальной в течение времени ). Время, показываемое часами в системе, относительно которой они покоятся, называется собственным. Ниже будем обозначать его  при использовании соответственно понятия интервал  и . Для собственного времени имеем выражение

                                                ,

                                                .

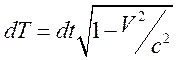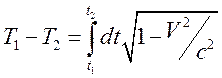Собственное время меньше, чем время в системах, движущихся относительно часов. Условие инвариантности интервала в рассматриваемой задаче имеет вид

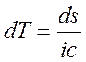                                    ,  или  ;

 ,  или .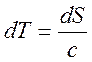

Собственное время является инвариантом.

12.3 Сложение скоростей. Аберрация света (аберрация - отклонение). Скорости частицы в системах  и  даются формулами

                                    ,         ,

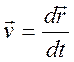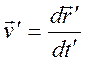Пусть система  движется с постоянной скоростью  вдоль оси  (), тогда согласно преобразованию Лоренца будем иметь

.

Разделив первые три равенства на четвертое, получим формулы для компонент скорости частицы

,    ,    

Если устремить скорость света к бесконечности, то получатся формулы сложения скоростей классической механики. Равномерное движение в одной инерциальной системе остается равномерным в любой другой инерциальной системе. Равноускоренное движение в одной инерциальной системе не является равноускоренным в других инерциальных системах. Если движение частицы происходит вдоль оси  (имеет место параллельное движение частицы и системы отсчета), то правило сложение скоростей имеет вид                                  

                                    .                                           (12.3)