Специальная теория относительности. Преобразования Лоренца. Промежуток времени между событиями. Длина отрезка. Лоренцово сокращение. Четырехмерное пространство Минковского. Интервал. Собственное время. Сложение скоростей, страница 4

Напомним, что  - скорость движения частицы и одновременно с этим, это скорость движения локально инерциальной системы .  произвольная функция времени, и при введении понятия собственного времени использовалось требование, чтобы движущаяся система  была бы «локально инерциальной» (инерциальной в течение бесконечно малого промежутка времени).

Таким образом, 4 – скорость определяется в виде

                                                            ,

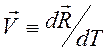где  - 4 – вектор,  - скаляр (инвариант), значит, ковариантная 4 – скорость  при переходе из одной инерциальной системы в другую должен преобразовываться  согласно преобразованию Лоренца:

                                                ,

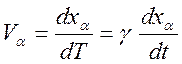где ,  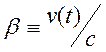, при  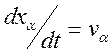  ,  - компоненты обычной 3 – скорости. Четвертая компонента  определяется соотношением

                                    .

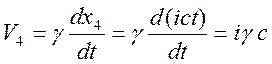В контравариантной форме будем иметь

            ,   ,  

Таким образом, имеем две формы записи для 4 – вектора скорости частицы

                                    ,                .

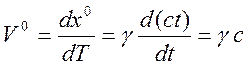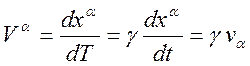Квадрат 4 - скорости имеет вид

                                    ,

т.е. является инвариантом. 4 – вектор скорости касателен к траектории движения точки в 4 – мерном пространстве – времени и он сохраняет свою величину (модуль).

            4 – ускорение определяется по формуле

                                    .

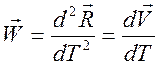Компоненты 4 – ускорения определяются в виде

,      ,

                        .

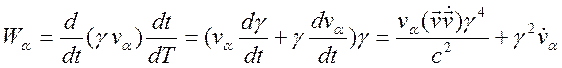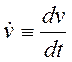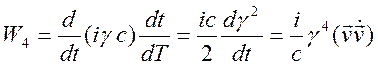В частном случае равномерного движения  и . Квадрат 4 - ускорения удовлетворяет соотношению

                                    .

Так как 4 – ускорение является производной от постоянного по величине (модулю) 4 – вектора скорости, то эти 4 – векторы ортогональны: ()=0. Этот факт может быть получен из эквивалентного представления. Дифференцируя по собственному времени  инвариантное соотношение

                                    ,

получим

                                    .

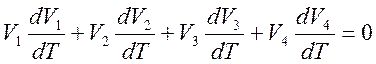            Это соотношение отражает отмеченный уже выше факт ортогональности 4 – скорости и 4 – ускорения: .

            2. Получим четырехмерное уравнение движения частицы. В классической механике второй закон Ньютона (уравнение движения) записывается в форме трехмерного векторного уравнения

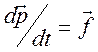                                                ,                                                       (12.4)

где  - трехмерный классический импульс частицы,  - масса покоя частицы,  - трехмерный вектор силы. Умножая (12.4) на , получим

                                                .

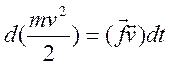Справа в этом соотношении стоит работа силы , значит, левая часть это изменение энергии. Энергию частицы можно записать в виде

                                                ,

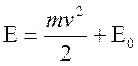где 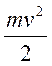 - кинетическая энергия частицы,  - энергия покоя, потенциальная или внутренняя энергия частицы. В классической механике .

            В релятивистской механике уравнение движения записывается в форме (12.4), но импульс  и сила  задаются в четырехмерном виде, а время заменяется собственным временем

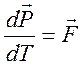                                                .                                                         (12.5)

4 – импульс вводится по определению , где  - масса покоя частицы, величина скалярная и поэтому инвариантная

                                           .

4 – силу  - в уравнении (12.5) еще нужно определить. В форме (12.5) уравнение движения инвариантно по отношению к преобразованию Лоренца. Учитывая, что 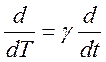 первые три компоненты уравнения движения (12.5) запишем в явном виде

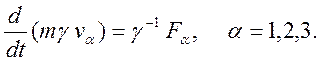                                                                   (12.6)

Если первые три компоненты 4 – силы  определим как , где  - обычная трехмерная сила, то с учетом такого определения (12.6) можно записать в векторной (трехмерной) форме аналогичной уравнению движения классической механики (12.4)

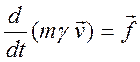                                    .                                                            (12.7)