На
самом деле, это уравнение по внешнему виду не отличается от уравнения движения
классической механики (12.4), если за трехмерный импульс принять величину ![]() . Отметим, что такой импульс в отличие от
импульса классического связан со скоростью частица нелинейным соотношением, так
как
. Отметим, что такой импульс в отличие от
импульса классического связан со скоростью частица нелинейным соотношением, так
как 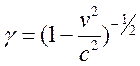 .
.
Рассмотрим
теперь четвертую компоненту уравнения движения (12.5), в котором не ясным
остается смысл компоненты силы ![]() . Оказывается, что она
может быть найдена по известным первым трем компонентам 4 – силы. Используем
отмеченный уже ранее факт ортогональности 4 – скорости и 4 – ускорения:
. Оказывается, что она
может быть найдена по известным первым трем компонентам 4 – силы. Используем
отмеченный уже ранее факт ортогональности 4 – скорости и 4 – ускорения: ![]() :
:
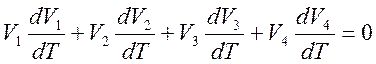 . (12.8)
. (12.8)
Примем
во внимание ![]() первые три компоненты уравнения движения
первые три компоненты уравнения движения
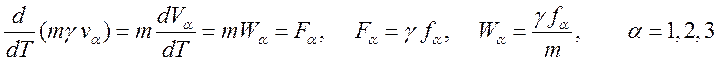
Для
четвертой компоненты имеем 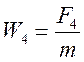 .
.
Соотношение (12.8) имеет вид
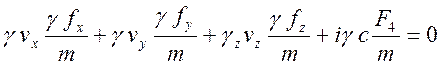 ,
,
позволяющим определить
![]() .
.
4
– сила ![]() называется силой Минковского
называется силой Минковского ![]() . Выясним физический смысл четвертой
компоненты уравнения (12.5):
. Выясним физический смысл четвертой
компоненты уравнения (12.5):
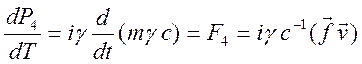 ,
,
или
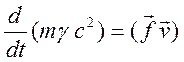 .
.
Справа здесь стоит работа силы в единицу времени, следовательно, слева в скобках должна стоять энергия (с точностью до постоянного слагаемого)
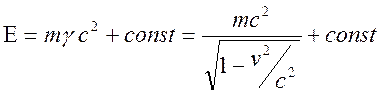 .
.
В
релятивистской механике делается выбор ![]() . Это
позволяет импульс
. Это
позволяет импульс ![]() и энергию
и энергию ![]() объединить в единый 4 – вектор импульса –
энергии. При этом энергия покоящейся частицы представляется в виде
объединить в единый 4 – вектор импульса –
энергии. При этом энергия покоящейся частицы представляется в виде
![]() .
.
Если
покоящаяся частица теряет при излучении энергию ![]() , то ее
масса покоя одновременно уменьшается на
, то ее
масса покоя одновременно уменьшается на
![]() .
.
Переход
из состояния покоя с энергией ![]() в состояние с энергией
в состояние с энергией ![]() приводит к изменению энергии на величину
приводит к изменению энергии на величину ![]() . Еще раз напомним, что в классической
механике
. Еще раз напомним, что в классической
механике ![]() . При переходе от собственной системы
отсчета (в ней частица покоится) к любой другой инерциальной системе энергия
возрастает в
. При переходе от собственной системы
отсчета (в ней частица покоится) к любой другой инерциальной системе энергия
возрастает в ![]() раз. В релятивистской механике
кинетическая энергия (энергия движения) получается вычитанием энергии покоя из
полной энергии
раз. В релятивистской механике
кинетическая энергия (энергия движения) получается вычитанием энергии покоя из
полной энергии
![]() .
.
3. Кроме инерциальных систем существует бесчисленное множество неинерциальных систем отсчета – систем движущихся с ускорением относительно инерциальных систем (такой системой является Земля, которая вращается вокруг своей оси, вокруг Солнца и вокруг центра нашей Галактики). Неинерциальными системами можно пользоваться при описании механических движений и любых физических процессов. Однако, инерциальные системы имеют преимущество простоты: свободное тело движется в них прямолинейно и равномерно. В неинерциальных системах возникают специфические силы: центробежная сила инерции, сила Кориолиса. Важнейшей особенностью сил инерции является то, что ускорение, вызываемое ими, не зависит от массы движущегося тела. По этой причине возникает аналогия между неинерциальными системами и гравитационными полями.
Пусть
неинерциальная система движется прямолинейно с постоянным ускорением ![]() относительно инерциальной системы. В ней
возникает сила инерции
относительно инерциальной системы. В ней
возникает сила инерции ![]() , где
, где ![]() - масса
тела. Если рассмотреть постоянное и однородное гравитационное поле с ускорением
- масса
тела. Если рассмотреть постоянное и однородное гравитационное поле с ускорением
![]() , то тело испытывает в нем действие силы
, то тело испытывает в нем действие силы ![]() . Если создать условие
. Если создать условие ![]() , то движение тела при наличии каких угодно
добавочных сил, в неинерциальной системе происходит точно так же, как движение
тела в инерциальной системе при наличии в ней гравитационного поля с ускорением
, то движение тела при наличии каких угодно
добавочных сил, в неинерциальной системе происходит точно так же, как движение
тела в инерциальной системе при наличии в ней гравитационного поля с ускорением
![]() . Неотличимость силы инерции,
возникающей в неинерциальной системе, движущейся прямолинейно и равномерно
ускоренно, от однородного гравитационного поля называют принципом эквивалентности.
Неинерциальные системы эквивалентны инерциальным системам с введением в них
некоторых гравитационных полей. В гравитационном поле пространство перестает
быть евклидовым. При этом геометрические свойства перестают быть абсолютными,
они зависят от гравитационных полей. Гравитационные поля создаются материей.
Поэтому геометрия пространства определяется материей. Геометрия пространства
теряет свое самостоятельное существование и становится частью физики. Это же
относится и ко времени. В этом состоит основная идея общей теории
относительности Эйнштейна (1915 г.).
. Неотличимость силы инерции,
возникающей в неинерциальной системе, движущейся прямолинейно и равномерно
ускоренно, от однородного гравитационного поля называют принципом эквивалентности.
Неинерциальные системы эквивалентны инерциальным системам с введением в них
некоторых гравитационных полей. В гравитационном поле пространство перестает
быть евклидовым. При этом геометрические свойства перестают быть абсолютными,
они зависят от гравитационных полей. Гравитационные поля создаются материей.
Поэтому геометрия пространства определяется материей. Геометрия пространства
теряет свое самостоятельное существование и становится частью физики. Это же
относится и ко времени. В этом состоит основная идея общей теории
относительности Эйнштейна (1915 г.).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.