Сигналы. Классификация и терминология. Периодические сигналы. Дискретные спектры. Непериодические сигналы. Сплошные спектры. Идеализированные сигналы. Обобщённые спектры, страница 9

Если аналоговый сигнал имеет математическую модель в виде непрерывной или кусочно-непрерывной функции , то соответствующий ему дискретный - это упорядоченная последовательность  значений функции в дискретные моменты времени . Практически выборки делаются с одинаковым интервалом , который называется шагом или интервалом дискретизации. Так проще (иначе пришлось бы запоминать и ), хотя и не всегда рационально. Значения  называют отсчётами или выборками аналогового сигнала, рис.2.27. Они задаются либо отрезками (ординатами), либо числами (таблица). Тогда дискретный сигнал называют цифровым.

Если аналоговый сигнал имеет ограниченный спектр и шаг дискретизации выбран правильно в соответствии с теоремой Котельникова, то мы можем восстановить аналоговый сигнал полностью по его выборкам, просуммировав ряд (2.25).

2.9.1.  Дискретизация аналогового сигнала.

Дискретизация есть процесс перехода к дискретному сигналу. Для этого надо измерить и запомнить отсчёты (ординаты) , представляющие значения аналогового сигнала . Приведённый рисунок 2.27 иллюстрирует этот процесс. Если аналоговый сигнал был записан ранее (график), то мы так и поступаем.

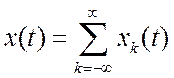Дискретизация аналогового сигнала непосредственно в процессе наблюдения производится путём перемножения сигнала  с дискретизирующей (или гребенчатой) функцией . Она представляет собой периодическую последовательность очень коротких прямоугольных импульсов с постоянной амплитудой  и длительностью , рис.2.28. Период этой последовательности  и определяет шаг дискретизации  (). Таким образом, , где  есть отдельный импульс с номером . Если устремить , при условии , то  превратиться в  функцию. . Тогда мы получим идеальную дискретизирующую функцию. Она не реализуема, но с нею гораздо проще работать на бумаге. Дальше мы будем писать формулы, в основном, для идеальной .

В результате перемножения сигнала  с реальной функцией  мы получим реальный дискретный сигнал в виде модулированной по амплитуде последовательности импульсов (уже не прямоугольных), изображённых на рис. 2.29. 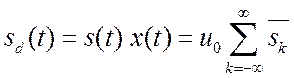, где  - это отдельные импульсы, амплитуда которых равна среднему значению  на интервале . Эта операция умножения часто называется стробированием.

После предельного перехода , будем иметь идеальный дискретный сигнал 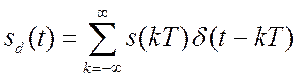. В результате, информация об аналоговом сигнале , заключённая в выборках , оказалась перенесённой на дискретизирующую последовательность.

2.9.2.  Спектр дискретного сигнала.

По нашему предположению аналоговый сигнал  имеет ограниченный спектр. Пусть он имеет вид, изображённый на рисунке 2.30. Определим спектр соответствующего дискретного сигнала .

Предварительно надо найти спектр дискретизирующей функции . Это периодическая функция, и её можно представить рядом Фурье (пример 2.2.1). 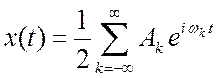, где 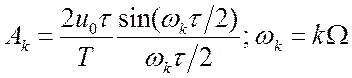. Значения  дают нам амплитуды гармоник дискретного спектра функции . Поскольку , число линий спектра до первого нуля огибающей будет велико. Рис. 2.31. Амплитуды гармоник убывают сначала очень медленно.

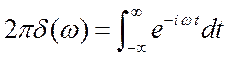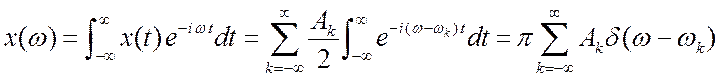Мы можем воспользоваться математическим формализмом и записать этот результат иначе, выразив спектр с помощью  функции. Делаем преобразование Фурье функции  (в обобщённом смысле, ).                       (2.28)
Получили тот же линейчатый спектр, только он записан удобнее для дальнейших вычислений. Если перейти к идеальной функции  (, ), то все  и мы получим 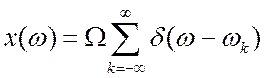 .                                       (2.29) Все гармоники имеют одинаковую амплитуду. Спектр равномерный.

Теперь мы легко можем получить спектр дискретного сигнала . Учтем следующее свойство преобразования Фурье. Спектр произведения сигналов есть свёртка спектров этих сигналов, делённая на . 

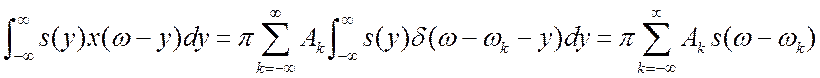.    (2.30)

Каков главный эффект?  При переходе к дискретному сигналу спектр стал периодическим с периодом . На рис. 2.32 ситуация изображена для идеальной функции  (). С ростом  (уменьшение ), копии спектра  будут дальше расходиться друг от друга. Правильное соотношение частот таково (), что копии спектра не перекрываются.