Сигналы. Классификация и терминология. Периодические сигналы. Дискретные спектры. Непериодические сигналы. Сплошные спектры. Идеализированные сигналы. Обобщённые спектры, страница 5

Если условно принять ширину спектра радиоимпульса  равной ширине главного максимума (по нулям), то . Отсюда , или . Когда  (как на рисунке), то сигнал получается узкополосным. Это ещё одна особенность спектров радиоимпульсов.

Пусть  МГц, а  сек. Тогда  Гц. Таким образом, включение генератора даже на одну секунду дает нам радиоимпульс, ширина спектра которого составляет единицы герц. Только уникальный анализатор сможет отличить сплошной спектр от линейчатого, длинный радиоимпульс - от чисто гармонического сигнала.

При анализе реальных сигналов мы всегда имеем дело со сплошным спектром, с линиями конечной ширины. Но часто, мы не можем определить ширину отдельной линии спектра, и поэтому воспринимаем спектр как линейчатый.

2.6.1.  Текущий спектр.

Проследим установление спектра радиоимпульса по мере его формирования. Воспользуемся результатом (2.17) и примем , целому числу периодов частоты заполнения. Тогда: 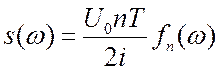; ; 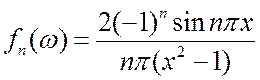; . На рис. 2.19 приведены графики  для .

Первый рисунок () дает спектр характерный для видеоимпульсов (широкополосный), в то время как последний () – это уже типичный узкополосный спектр радиоимпульса с чётко выраженным главным максимумом на частоте заполнения. Он будет тем ýже, чем больше периодов содержит импульс.

Этот пример подводит нас к очень важному понятию текущего спектра

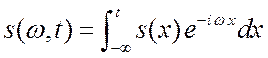.                                                                                 (2.18)
Обычный спектр характеризует весь импульс в целом и не зависит от времени. Он получится, когда импульс уже кончился. Текущий спектр отражает процесс формирования импульса, и сам формируется, меняется со временем. Приведенные рисунки фактически показывают нам текущие спектры длинного радиоимпульса в определённые моменты времени, через 1,2,4 и 10 периодов после включения.

Точно так же формируется и спектр видеоимпульса, например, прямоугольного. Сразу после включения импульса спектр широкий, но по мере формирования импульса он сужается, приближаясь к установившемуся.

2.6.2.  Гармонический сигнал.

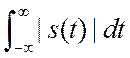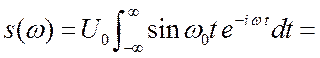
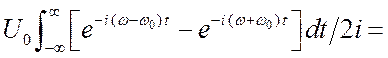
Рассмотрим теперь чисто гармонический сигнал и проиллюстрируем использование аппарата  - функции. Пусть .  расходится, спектр получится обобщённый.  . Здесь мы учли равенство 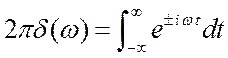. Поскольку сигнал периодический и содержит одну гармоническую составляющую, можно было сразу нарисовать его спектр - одну линию. К этому же нас привела и формальная процедура использования преобразования Фурье с обобщёнными спектрами. Такое представление дискретного спектра иногда оказывается более удобным. Обратное преобразование дает снова .

2.6.3.  Бесконечно длинный радиоимпульс.

. Сигнал идеализирован, спектр получится обобщённый. Воспользуемся сразу преобразованием Лапласа.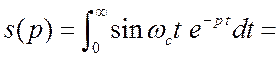

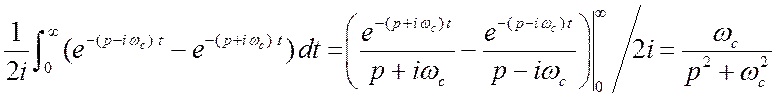.           (2.19)
Первообразная функция на верхнем пределе равна нулю, поскольку . Полагая , получим обобщённый спектр Фурье .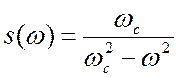

2.7.  Модулированные сигналы.

Гармонический сигнал  содержит три параметра: Амплитуда , частота  и фаза . Для передачи информации какой-то из этих параметров надо менять, модулировать. Различают амплитудную и угловую модуляцию. Последняя делится на два трудно различимых вида, частотную и фазовую. Проанализируем спектры таких сигналов.

2.7.1.  Амплитудная модуляция.

Постоянная фаза  ничего не меняет и её можно опустить. Рассмотрим сначала простейший пример периодического изменения  по гармоническому закону, рис. 2.20. .

Параметр  определяет глубину модуляции;  называют несущей частотой, а  есть частота модуляции. Обычно .  . Простые тригонометрические преобразования дают: 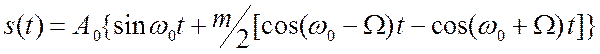.                          (2.20)

Таким образом, рассматриваемый сигнал образуют три гармонические составляющие с частотами  и , рис. 2.21. Спектр получился дискретный и состоит из трёх линий, основной и боковых. Сигнал в целом может быть периодическим или непериодическим, если  и  находятся в иррациональном отношении. Однако это совсем не важно. Ширина спектра равна . Если , то сигнал узкополосный.