Сигналы. Классификация и терминология. Периодические сигналы. Дискретные спектры. Непериодические сигналы. Сплошные спектры. Идеализированные сигналы. Обобщённые спектры, страница 7

Обратимся снова к гармоническим сигналам и приведём некоторые наводящие соображения. Пусть  и . Эти вещественные сигналы получаются из комплексного сигнала , если взять реальную и мнимую части последнего, и называются сопряжёнными. Комплексному сигналу сопоставляется вектор  на комплексной плоскости, который вращается с угловой частотой . Вещественные сигналы  и  являются проекциями этого вектора на оси  и  соответственно, рис. 2.24. Длина вектора , равная , и есть амплитуда сигнала, которая нас интересует, а угол  - аргумент тригонометрических функции, причём .

Для чисто гармонического сигнала (амплитуда постоянна) сопряженный сигнал не нужен. В общем случае нужны два сигнала, две проекции вектора, чтобы определить его однозначно. Так и поступают. Сначала по заданному сигналу  находят другой сигнал , сопряженный данному (другая проекция вектора). Потом определяют 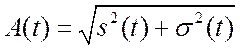 и .

Теперь возникла проблема определения сопряжённого сигнала. Для гармонических сигналов проблемы нет. Если , то . Если , то . Чтобы получить сопряжённый сигнал, надо исходный сместить на четверть периода вправо (запаздывание). Приведённые рисунки 2.24 и 2.25 поясняют сказанное. Для суммы гармонических сигналов проблемы тоже нет. Пусть ; ; . Тогда .

Другой пример. Имеем узкополосный амплитудно - модулированный сигнал . Тогда  есть сопряжённый данному. . Амплитуда одинакова для  и . Отличаются они только фазами несущей частоты .

Теперь уже можно сформулировать алгоритм и для общего случая.

1. Представляем заданный сигнал  рядом или интегралом Фурье. Другими словами, находим спектр .

2. Для каждой спектральной составляющей находим сопряженный сигнал.

3. Путем суммирования (или интегрирования) находим общий сопряжённый сигнал .

4. Определяем  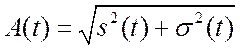и .

В итоге: . Можем написать и комплексный сигнал, если это необходимо. .

2.7.4.  Свойства функции . Огибающая.

Рассмотрим два равенства: ; . Второе получается из первого после возведения его в квадрат и дифференцирования. Будем считать . Выберем момент , когда , а , рис. 2.26. Из двух равенств следует: . Если ещё учесть неравенство , то становится очевидным, что  и  не пересекаются, а только касаются. Поэтому говорят, что  есть огибающая сигналов  и . Оба эти сигнала равноправны по отношению к . Чем медленнее меняется , тем ближе точки касания  и  к точкам экстремумов .

2.7.5.  Некоторые дополнительные результаты.

В математике понятие сопряжённых функции используется давно. В строгой теории сигналов тоже отмечается более общий характер связи между сопряженными сигналами. Оказывается,  и  связаны преобразованиями Гильберта, как вещественная и мнимая части комплексного сигнала .

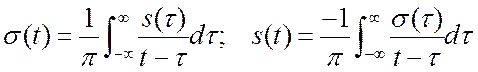.                                                   (2.23)
Такое определение  даёт возможность вычислять сопряженный сигнал непосредственно, не переходя к спектрам. Всё сказанное ранее остаётся в силе. Например, пусть . Определим .

.

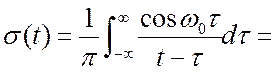
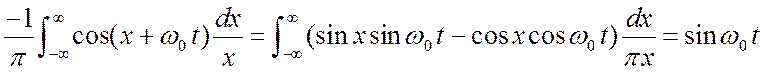В заключение вычислим спектры сигналов  и . Пусть сигналу  соответствует спектр . Каков спектр сопряжённого сигнала ?

/
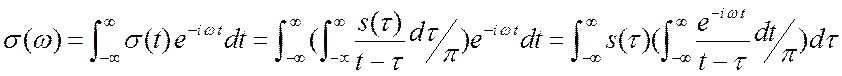Изменили порядок интегрирования. Внутренний интеграл вычислим отдельно.

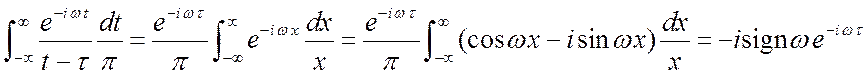
В итоге, 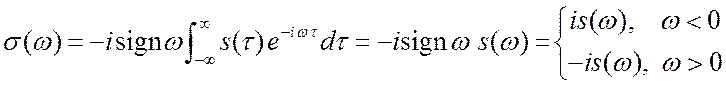. (2.24)

Спектр комплексного сигнала  оказывается интересным.

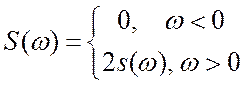. Этот результат позволяет определить , минуя определение . .

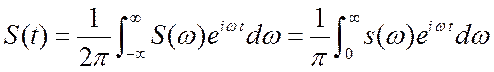2.8.  Дискретизация аналоговых сигналов. Теорема Котельникова.

Дискретизация сигналов представляет чрезвычайно важную операцию превращения аналогового сигнала в дискретный, в последовательность равноотстоящих отсчётов функции с интервалом дискретизации . На следующем этапе обработки дискретный сигнал обычно превращают в цифровой (оцифровывание), в таблицу значений, которая вводится прямо в память компьютера. Все дальнейшие необходимые операции с сигналом производит уже компьютер. Такова современная методика обработки сигналов.