Сигналы. Классификация и терминология. Периодические сигналы. Дискретные спектры. Непериодические сигналы. Сплошные спектры. Идеализированные сигналы. Обобщённые спектры, страница 4

2.5.1.  Ступенчатая функция (функция Хевисайда).

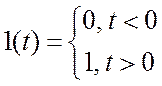. Рис. 2.13а. Непосредственно по приведённым формулам получить обычный спектр  нельзя. 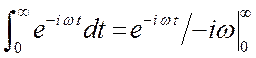 ? Первообразная функция на верхнем пределе не определена ( вещественно).

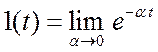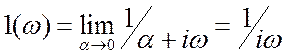В математике обобщённые функции часто получают путём предельного перехода от обычных. Поступим так же. Ступенчатую функцию можно получить из экспоненциальной.  , при . Следовательно .  (2.12)
Плотность спектра имеет особенность при . Это уже обобщённый спектр, и с ним надо быть осторожным. Тем не менее, многие примеры можно рассматривать с этим спектром, забывая, что он обобщённый.

Другой путь получения обобщённых спектров базируется на преобразовании Лапласа, которое обычно используется для функции , при .

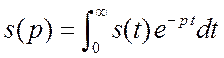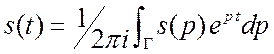;       .                                        (2.13)
Контур  проходит в правой полуплоскости комплексной переменной , рис. 2.13б. Условие  обеспечивает сходимость интеграла. Для применимости этого преобразования ограниченность интеграла 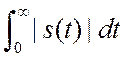 не нужна. Функция может даже расти при .

При переходе от преобразования Фурье к преобразованию Лапласа, мы  заменяем на комплексный параметр , считая . Для ступенчатой функции: 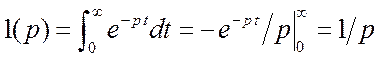. Заменив теперь  обратно на , получим обобщённый спектр по Фурье.

Ступенчатая функция очень широко используется при анализе цепей (да и вообще в физике) для выяснения реакции цепи на резкие изменения входного сигнала. Однако роль этого сигнала велика ещё и потому, что любой сигнал можно приближённо, а в пределе точно, представить набором ступенек. Например, прямоугольный импульс получается наложением двух ступенек.
, рис. 2.13а. Соответственно, спектр (он уже нормальный, не обобщённый) 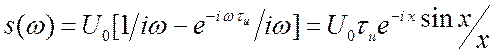, где . Множитель  учитывает запаздывание импульса на время . К этому мы ещё вернёмся.

2.5.2.  Предельно короткий прямоугольный импульс.

Форма импульса здесь не принципиальна; выбор сделан для определённости. Пусть импульс прямоугольный, рис. 2.14, и . Сделав предельный переход , мы придем к  - функции. Это тоже сигнал с неограниченной энергией. Для рассматриваемого импульса , где . После предельного перехода получим 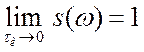. Плотность спектра  - функции оказалась одинаковой для всех частот (равномерный спектр). Этот результат можно получить и непосредственно, исходя из свойств  - функции. 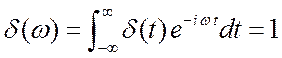.Если мы имеем , то .

Однако мы получили опять обобщённый спектр. Это проявится, как только мы напишем обратное преобразование. 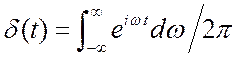.                 (2.14)
Такой интеграл может быть воспринят только в обобщённом смысле.

Говоря о роли таких предельно коротких импульсов, можно, фактически, повторить всё, что сказано о роли ступенчатой функции.

2.5.3. Функция , где .

В заключение рассмотрим эту интересную функцию, рис. 2.15, и найдём её спектр. Строго говоря, 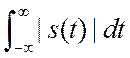 расходится, однако при вычислении спектра это никак не проявляется.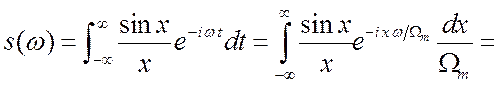

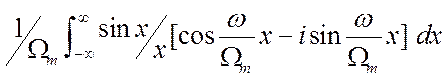. Интеграл от второго слагаемого равен нулю в силу нечётности подынтегральной функции. После тригонометрических преобразований имеем:

.(2.15)
Здесь мы учли следующее: .

 Спектр получился равномерным в ограниченной полосе частот от 0 до , рис. 2.16. Таким образом, параметр  есть предельная частота в спектре этого сигнала. Если 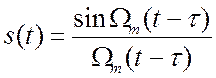, то 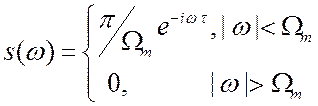.                  (2.16)

Рассмотренная функция нам понадобится позже, когда мы будем обсуждать теорему Котельникова. Отметим, что этот пример, вместе с примером 2.4.1, ещё раз иллюстрирует симметрию преобразования Фурье.

2.6.  Спектр радиоимпульса с прямоугольной огибающей.

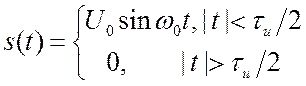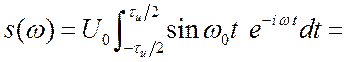
. Рис. 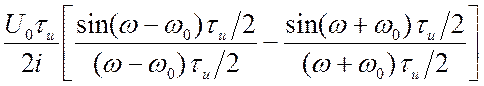2.17.

. (2.17)
Спектр получился сплошной. Качественная картина спектра изображена на рисунке 2.18 для случая, когда радиоимпульс содержит много периодов  частоты  . Спектр имеет главный максимум на частоте  и убывающие, по мере удаления от главного, побочные. Спектр радиоимпульса фактически получился смещением спектра прямоугольного видеоимпульса (огибающей) на частоту . В этом и состоит главное отличие спектров видеоимпульсов и радиоимпульсов.