Сигналы. Классификация и терминология. Периодические сигналы. Дискретные спектры. Непериодические сигналы. Сплошные спектры. Идеализированные сигналы. Обобщённые спектры, страница 3

2.4.2.  Экспоненциальный импульс.

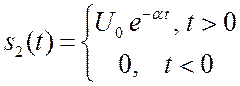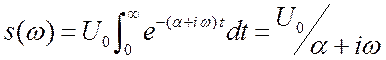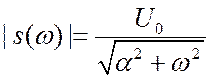. .   (2.9)
Импульс и его спектр изображены на рисунках 2.9 и 2.10. Длительность импульса на уровне равна .  убывает монотонно с ростом , но достаточно медленно. Для определения ширины спектра примем уровень 0,1 от . Тогда:; .

2.4.3.  Косинусоидальный импульс (непрерывный).

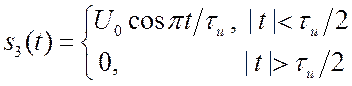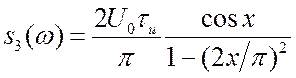.  ;  .   (2.10)
Импульс и его спектр изображены на рис. 2.7 и 2.8.  есть "площадь" импульса.  убывает с ростом  немонотонно, но уже быстрее, как  (сигнал непрерывен). Ширина спектра до первого нуля  равна . Тогда .

2.4.4.  "Колокольный" импульс (гладкий).

. Рис. 2.11. Сигнал бесконечен во времени, но он очень быстро стремится к нулю с ростом . Поэтому он служит хорошей моделью гладкого импульса конечной длительности. Длительность импульса условно (для оценок) определяется на уровне . Тогда . Вычислим спектр этого сигнала.

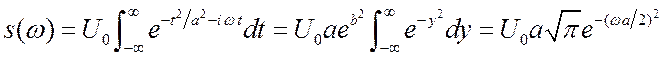 (),  (2.11)
где  выбирается из условия . Последний интеграл равен .  есть "площадь" импульса. Плотность спектра, рис. 2.12, определяется такой же функцией, как и импульс, и очень быстро, монотонно убывает с ростом . Определим условно ширину спектра  тоже на уровне . Тогда  или .

2.4.5.  Связь длительности импульса и ширины спектра.

Из приведённых примеров следует, что произведение длительности импульса  на ширину спектра  даёт величину порядка единицы. Интересно определить для какого импульса это произведение будет минимальным. Важность этого вопроса связана с выбором оптимальной формы импульса для кодирования информации.

Предварительно мы должны принять некоторый единый, удобный способ определения длительности импульса и ширины спектра. Такой общий способ был предложен на энергетической основе. Для всех рассмотренных импульсов, кроме последнего, мы можем считать  при . "Колокольный" импульс описывается четной функцией времени, и при вычислении полной энергии сигнала мы можем снова интегрировать по промежутку , удвоив результат. Тогда полная энергия сигнала ( для "колокольного" и  для всех остальных импульсов)  .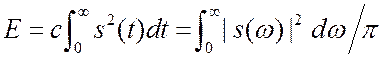

При интегрировании по конечным интервалам мы получим часть полной энергии. Определим длительность импульсов  и ширину спектров   так, чтобы получить, например, 0,9 полной энергии из равенств: 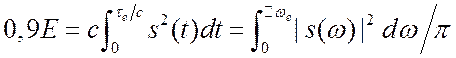. Теперь можно сравнивать произведения . Интересные результаты такого сравнения приведены в таблице, которая заимствована из книги Харкевича «Спектры и анализ».

Импульсы с разрывами самые плохие. Непрерывные импульсы лучше. При той же эффективной длительности их спектр примерно в два раза уже. Для "гладких" импульсов спектр будет ещё уже, но всегда . Значение произведения для колокольного импульса получается очень близким к теоретическому пределу.

2.5.  Идеализированные сигналы. Обобщённые спектры.

При анализе линейных цепей широко используются идеализированные сигналы, которые не могут быть реализованы, такие, как ступенчатая функция (прямоугольный импульс бесконечной длительности), предельно короткий импульс -  функция, линейно растущее (неограниченно) напряжение и другие. Несмотря на это, первые два сигнала находят очень широкое применение по причинам, которые скоро станут понятны. Такие сигналы не удовлетворяют условию абсолютной интегрируемости, их энергия бесконечна. Приходится вводить обобщенные спектры, поскольку обычное преобразование Фурье для них неприменимо.