С
каким интервалом ![]() надо производить дискретизацию,
чтобы не потерять информацию? Ответ даёт теорема Котельникова. Если мы имеем
сигнал с ограниченным спектром (
надо производить дискретизацию,
чтобы не потерять информацию? Ответ даёт теорема Котельникова. Если мы имеем
сигнал с ограниченным спектром (![]() при
при ![]() ), то
), то
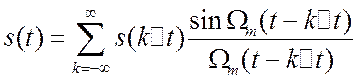 ,
(2.25)
,
(2.25)
где ![]() , а
, а ![]() есть
максимальная частота, представленная в спектре сигнала
есть
максимальная частота, представленная в спектре сигнала ![]() .
Замечательное свойство этого разложения состоит в том, что его коэффициенты
есть значения самой функции
.
Замечательное свойство этого разложения состоит в том, что его коэффициенты
есть значения самой функции ![]() в дискретные моменты
времени. Зная этот дискретный набор значений, мы можем полностью (точно)
восстановить функцию
в дискретные моменты
времени. Зная этот дискретный набор значений, мы можем полностью (точно)
восстановить функцию ![]() в любой другой момент времени.
в любой другой момент времени.
Реальный сигнал фактически имеет ограниченный спектр, поэтому он может быть представлен таким разложением.
2.8.1. Доказательство теоремы Котельникова.
Написанное выше разложение есть обобщённый ряд Фурье
по функциям ![]() , где
, где ![]() . Каждая
последующая функция
. Каждая
последующая функция ![]() получается из предыдущей путём
смещения на
получается из предыдущей путём
смещения на ![]() вправо (запаздывание), рис. 2.15. Эти
функции образуют полную ортогональную систему на бесконечном интервале.
вправо (запаздывание), рис. 2.15. Эти
функции образуют полную ортогональную систему на бесконечном интервале. 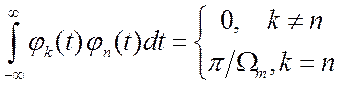 . (2.26)
. (2.26)
Покажем это. Пусть: ![]() и
и ![]() ;
; ![]() . Тогда
. Тогда
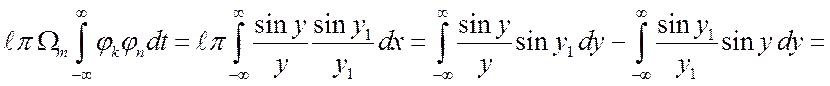
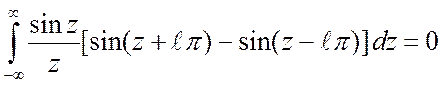
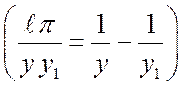 , поскольку аргументы синусов в квадратных
скобках отличаются на
, поскольку аргументы синусов в квадратных
скобках отличаются на ![]() .
.
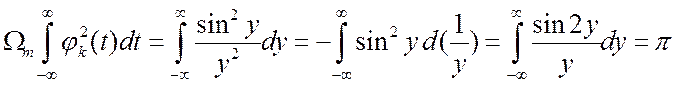 .
.
Раньше (пункт 2.5.3) мы вычисляли уже спектр функции ![]() и получили
и получили ![]()
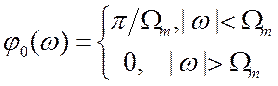 . Тогда
. Тогда 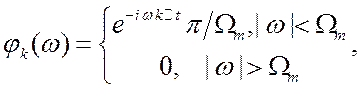 поскольку
функции
поскольку
функции ![]() получаются из
получаются из ![]() путём
сдвига на
путём
сдвига на ![]() в сторону запаздывания. Все функции
в сторону запаздывания. Все функции ![]() есть функции с ограниченным спектром.
есть функции с ограниченным спектром.
Если нам задан сигнал ![]() с
ограниченным спектром, удовлетворяющий условиям Дирихле на любом конечном
интервале и такой, что
с
ограниченным спектром, удовлетворяющий условиям Дирихле на любом конечном
интервале и такой, что 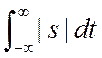 ограничен, то мы можем
представить этот сигнал обобщённым рядом Фурье по функциям
ограничен, то мы можем
представить этот сигнал обобщённым рядом Фурье по функциям ![]() .
. 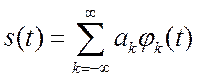 .
(2.27)
.
(2.27)
Для нахождения коэффициентов ![]() нужно обе части этого
равенства умножить на
нужно обе части этого
равенства умножить на ![]() и интегрировать по всему
промежутку. При этом в силу ортогональности функции
и интегрировать по всему
промежутку. При этом в силу ортогональности функции ![]() и
и ![]() , в правой части останется одно слагаемое
ряда с
, в правой части останется одно слагаемое
ряда с ![]() и мы получим
и мы получим 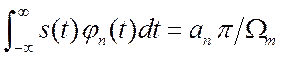 .
Вычислим этот интеграл.
.
Вычислим этот интеграл.
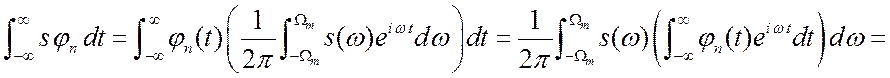
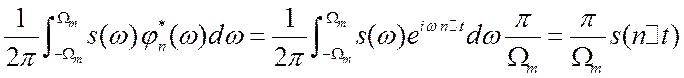 .
.
Здесь мы учли равенства: 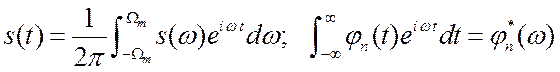 .
.
В итоге, ![]() . Этот результат можно было получить проще.
В самом деле, коэффициенты
. Этот результат можно было получить проще.
В самом деле, коэффициенты ![]() не зависят от времени,
поэтому для их определения в разложении (2.27) надо положить
не зависят от времени,
поэтому для их определения в разложении (2.27) надо положить ![]() . Тогда от суммы останется всего один член
ряда с
. Тогда от суммы останется всего один член
ряда с ![]() , поскольку
, поскольку ![]() , если
, если ![]() ;
; ![]() .
.
Сформулируем ещё раз результат, в силу его важности.
Сигнал с ограниченным спектром мы можем точно представить его выборками,
дискретными отсчётами с интервалом ![]() . Эти отсчёты и
являются коэффициентами ряда Котельникова.
. Эти отсчёты и
являются коэффициентами ряда Котельникова.
Для практики самым ценным результатом теоремы
Котельникова является возможность точного представления функции выборками и
конкретное значение интервала дискретизации ![]() . В
реальной ситуации мы редко знаем максимальную частоту в спектре сигнала точно.
Однако всегда можно оценить её косвенно, учитывая конкретные особенности
источника сигнала. Огромное значение имеет опыт работы с подобными сигналами.
. В
реальной ситуации мы редко знаем максимальную частоту в спектре сигнала точно.
Однако всегда можно оценить её косвенно, учитывая конкретные особенности
источника сигнала. Огромное значение имеет опыт работы с подобными сигналами.
2.9. Дискретные сигналы.
Мы рассмотрели некоторые типичные аналоговые сигналы. Теперь очень коротко остановимся на особенностях дискретных сигналов.
Исходный сигнал, как правило, является аналоговым. Тем не менее, часто информация поступает к нам сразу в виде отдельных выборок, в дискретном виде. Таковы физические, метеорологические "рутинные" измерения через определённые интервалы времени; производственные и экономические показатели и другие. Однако в последнее время быстро развивается тенденция превращать и аналоговые сигналы в дискретные. Здесь несколько причин.
1. Объём дискретной информации меньше. Проще хранить.
2. Дискретный сигнал удобнее обрабатывать с помощью ЭВМ. Таблица отсчётов вводится в компьютер и производится необходимая обработка.
3. Потери и искажение информации при хранении (старение) и передаче дискретного сигнала (цифрового) меньше. Информация сохраняется лучше, полнее.
Поэтому дискретные сигналы используются всё шире и шире.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.