Квазистационарные явления в электродинамике. Потенциалы, описывающие квазистационарные поля. Теория цепей, как частный случай квазистационарного приближения, страница 8

В частности, в линии без потерь () система (9.32) и (9.33) приводится дифференциальному уравнению второго порядка для  и для :

                        ,              ,                   .

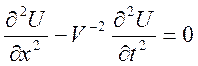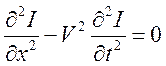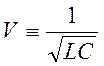Здесь  - скорость распространения волны напряжения и волны тока. Общее решение этих уравнений имеет вид

                        ,                       ,

где  - произвольные функции. Функции  описывают волны, распространяющиеся в направлении , а функции  описывают волны, распространяющиеся в сторону .

            Получим связь между волнами, распространяющимися в одну сторону, например . Из второго телеграфного уравнения (9.33) имеем

                                                            .

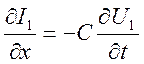Переходя к переменной , получим обыкновенное дифференциальное уравнение

                                                .

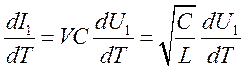Интегрируя это уравнение и полагая равной нулю константу интегрирования, получаем связь волны напряжения с волной тока

                                                .

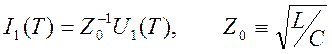Параметр  имеет размерность сопротивления и называется волновым сопротивлением линии передачи. Для волн, перемещающихся в обратном направлении, имеет место связь

                                                .

            Большое применение имеет двухпроводная линия в виде коаксиального кабеля. Для него были получены формулы для емкости и индуктивности элемента  длины и для единицы длины кабеля

                                    ,

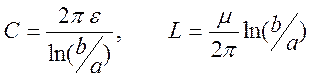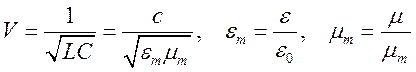где  - диэлектрическая и магнитная проницаемости среды между внутренним и внешним проводниками ( - их диаметры). Скорость распространения волн в кабеле представляется в виде ,   - скорость света в вакууме. Таким образом, за счет выбора среды заполнения можно замедлять скорость распространения волн в кабеле. Волновое сопротивление кабеля представляется в виде

                                               

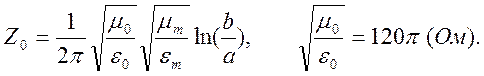
9.9. Гармонический процесс в длинной линии. Общее решение уравнения для напряжения в длинной линии без потерь представляется суммой двух волн, распространяющихся в противоположных направлениях

                                                .

Частным случаем таких волн являются гармонические волны

                                   

где  - произвольные постоянные, ниже возьмем . Учитывая связь волн тока с волнами напряжения, имеем

Таким образом, общее решение телеграфных уравнений в данной задаче имеет вид

где  - две произвольные константы.

            Рассмотрим конкретную ситуацию: процесс в полу бесконечной линии с сопротивлением нагрузки  при  (Рис. 9.9). В этой точке должно выполняться условие 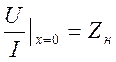, которое дает 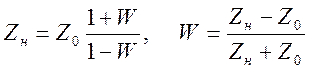. Параметр  имеет смысл коэффициента отражения волны напряжения. Рассмотрим предельные случаи:

1). .

2). .

3). .

            Рассмотрим теперь процесс в линии конечной длины. На концах линии задаем условия

                                                   .

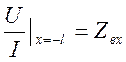
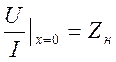Получаем

                                    ,

                                    .

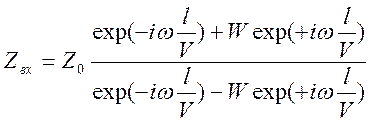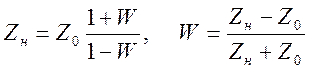Рассмотрим предельные случаи:

1).

2).

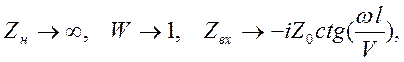
3).

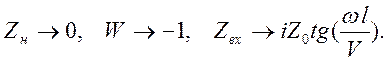
При  и  входное сопротивление длинной линии чисто мнимое и изменяется периодически при изменении длины линии (период находится из условия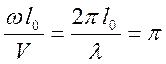). Область  соответствует емкостному сопротивлению, а область  соответствует индуктивному сопротивлению.

            В заключение изобразим эпюры напряжений в разомкнутой линии в разные моменты времени после подключения источника напряжения. Эта ситуация выходит за рамки рассмотрения гармонических процессов. Коэффициент отражения для напряжения от разомкнутого конца линии . Считается, что источник не имеет внутреннего сопротивления. Коэффициент отражения волны напряжения от источника (от короткого замыкания) . (Рис.9.10). Имеет место периодический процесс.