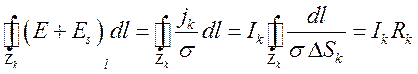Квазистационарные явления в электродинамике. Потенциалы, описывающие квазистационарные поля. Теория цепей, как частный случай квазистационарного приближения, страница 4

                                                ,            (9.16)

где 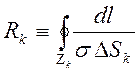 - сопротивление контура ,   - падение напряжения на сопротивлении контура, 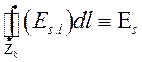 -электродвижущая сила (ЭДС). Падение напряжения зависит от величины сопротивления  и не зависит от распределения плотности сопротивления по длине контура. По этой причине можно считать, что сопротивление  сосредоточено в некотором произвольном месте контура. Следствием уравнения 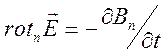 является то, что циркуляция вектора  связана с изменением магнитного потока 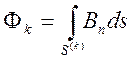 ( - площадь поверхности, ограниченной замкнутым контуром ) формулой

                                                            .

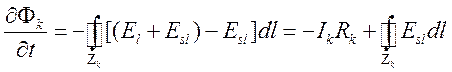Соотношение (9.16) перепишем в виде

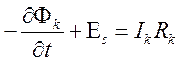                                                .                                         (9.17)

Контурный интеграл в (9.17) представляет собой стороннюю Э.Д.С. , поэтому (9.17) для замкнутого контура представляется в виде

                                                .

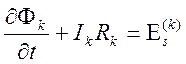            В случае разомкнутого проводника, когда в месте разрыва подключена емкость  (Рис. 9.1), интеграл по замкнутому контуру  от  можно записать в виде

                        .

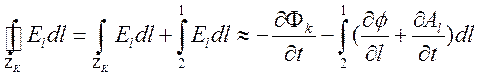В этом выражении пренебрежем слагаемым 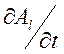 по сравнению с 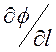, поскольку электрическое поле в конденсаторе определяется в основном разностью потенциалов , а не изменением магнитного поля. Интегрирование в 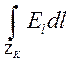 производится по незамкнутому контуру. Имеет место приближенное представление .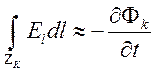

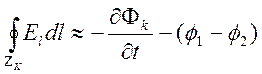                                        .                                   (9.18)

Учтем представления для взаимной индуктивности и емкости:

                                   

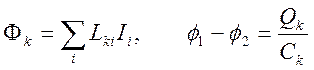
и уравнения (9.16) и (9.18) объединим в виде

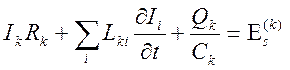                                    .                                   (9.19)

Это второй закон Кирхгофа.

            Первый закон Кирхгофа является следствием уравнения (в квазистационарном приближении при выполнении условия)

                                                .

Имеем следствие

                                                .

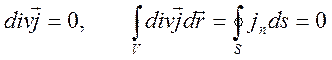Если применить последнее равенство к узлу токов (Рис. 9.3), то придем к первому закону Кирхгофа

                                                            ,

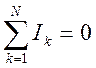в котором, токи, вытекающие из узла считаются положительными, а втекающие - отрицательными.

            Следует отметить, что законы Кирхгофа не могут быть получены на основе только уравнений Максвелла, так как для их получения необходима не содержащаяся в уравнениях Максвелла информация (сопротивления, емкости и индуктивности цепей). Уравнения Кирхгофа по этой причине качественно отличаются от уравнений Максвелла.

9.5. Скин – эффект. Выше не принималось во внимание распределение переменных токов по сечению проводников. На самом деле это распределение важно не только с теоретической точки зрения, но и с технической точки зрения. Ниже будет показано, что переменный ток в проводнике, в отличие от постоянного тока не распределяется равномерно по сечению проводника, а концентрируется на его поверхности. Это явление называется скин – эффект (от английского слова skin - кожа). Переменный ток как бы «выдавливает» сам себя к поверхности проводника. Это влечет за собой изменение эффективного сопротивления и самоиндукции проводника. Эти величины зависят от времени, в случае гармонических полей имеется зависимость от частоты тока. Точное решение задачи о скин – эффекте  достаточно сложно – имеется зависимость не только от формы проводника, но и от способа возбуждения в нем тока.

            Рассмотрим задачу о возбуждении тока гармоническим полем (рассмотрение проведем в комплексной форме, по существу можно считать, что речь идет о фурье – образе поля)  в цилиндрическом проводнике радиуса  (Рис. 9.4). Проводимость проводника  и его магнитную проницаемость считаем постоянными. Задачу будем решать в цилиндрической системе координат  с учетом осевой симметрии 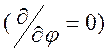. Длину проводника считаем бесконечной, свойства полей считаем не зависящими от координаты . Связь плотности тока с полем дается локальным соотношением (рассматриваем Фурье-образы полей)