![]() ,
,
где ![]() -
скорость поступательного движения, а
-
скорость поступательного движения, а ![]() - угловая скорость
вращения тела. Найдем ускорение
- угловая скорость
вращения тела. Найдем ускорение 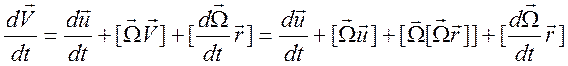 .
.
Рассматривается задача о движении
проводника как целого (без деформаций), поэтому первые два слагаемые в правой
части не зависят от координат. Третий член представляется в виде градиента 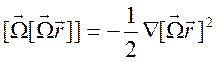 . Формула (9.28) преобразуется к виду
. Формула (9.28) преобразуется к виду
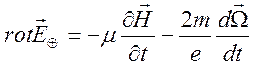 ,
,
где учтено соотношение 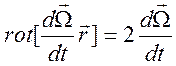 .
.
Введем обозначение 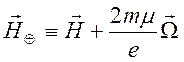 и получим уравнение
и получим уравнение
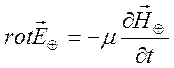 . (9.29)
. (9.29)
Так как ![]() не
зависит от координат, то уравнение
не
зависит от координат, то уравнение ![]() можно записать в виде
можно записать в виде
![]() . (9.30)
. (9.30)
Уравнения (9.29) и (9.30) приводятся к уравнению для квазистационарных процессов в неподвижном проводнике
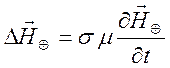 .
.
Вне проводника квазистационарный
процесс (предполагается, что длина волны больше размеров тела) описывается
уравнением ![]() . На поверхности проводника непрерывны оба
вектора
. На поверхности проводника непрерывны оба
вектора ![]() и
и ![]() . На
бесконечности
. На
бесконечности ![]() ,
, 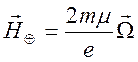 .
.
Переменное магнитное поле индуцирует в проводнике электрический ток. В неравномерно вращающемся кольце возникает Э.Д.С. (эффект Стюарта - Толмэна).
9.8.
Электромагнитные волны в линиях передачи. Телеграфные уравнения. Решение задач о распространении волн вдоль проводников
связано с определенными трудностями. В электротехнике быстрых токов
используется упрощенный (нестрогий) способ рассуждений, приводящий к
приближенно правильным результатам. Для описания быстропеременных токов
используется неприменимая для этого теория токов квазистационарных. При этом
рассматривается не вся цепь в целом, а отдельные малые ее участки длины ![]() . Предполагается, что квазистационарное
описание применимо к каждому такому участку.
. Предполагается, что квазистационарное
описание применимо к каждому такому участку.
Рассмотрим
задачу о распространении волн в двухпроводной линии (система Лехера),
состоящей из двух параллельных проводников (Рис. 9.6). Будем интересоваться
случаем, когда длина линии ![]() и ее поперечный размер
и ее поперечный размер ![]() удовлетворяют условиям
удовлетворяют условиям ![]() (здесь
(здесь ![]() - длина
волны). Условие квазистационарности не выполняется относительно длины линии
- длина
волны). Условие квазистационарности не выполняется относительно длины линии ![]() . Не смотря на это, выделим малый участок
линии длиной
. Не смотря на это, выделим малый участок
линии длиной ![]() (Рис. 9.7) и на нем используем
квазистационарное описание. Введем понятие напряжения между точками 1 и
2:
(Рис. 9.7) и на нем используем
квазистационарное описание. Введем понятие напряжения между точками 1 и
2:
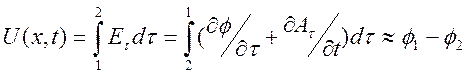 . (9.31)
. (9.31)
В
определении (9.13) интегрирование производится по поперечной к ![]() координате. При написании (9.31) сделано
пренебрежение влиянием изменения магнитного поля, использовано приближение
координате. При написании (9.31) сделано
пренебрежение влиянием изменения магнитного поля, использовано приближение 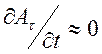 . Это соответствует пренебрежению явлением
электромагнитной индукции. Выделенный элемент системы характеризуем
сопротивлением
. Это соответствует пренебрежению явлением
электромагнитной индукции. Выделенный элемент системы характеризуем
сопротивлением ![]() , емкостью
, емкостью ![]() и коэффициентом самоиндукции
и коэффициентом самоиндукции ![]() , где
, где ![]() -
удельные величины (на участке линии единичной длины) сопротивления, емкости и
самоиндукции. При наличии утечки между проводами вводится понятие проводимости
-
удельные величины (на участке линии единичной длины) сопротивления, емкости и
самоиндукции. При наличии утечки между проводами вводится понятие проводимости ![]() Эквивалентная схема участка линии может
быть представлена в виде, изображенном на Рис. 9.8. Второй закон Кирхгофа для
такой схемы дает
Эквивалентная схема участка линии может
быть представлена в виде, изображенном на Рис. 9.8. Второй закон Кирхгофа для
такой схемы дает
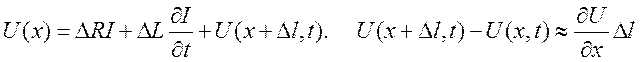 .
.
Разделив
на ![]() , получим первое телеграфное уравнение
, получим первое телеграфное уравнение
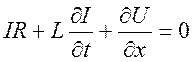 . (9.32)
. (9.32)
Второе
телеграфное уравнение напишем, применяя первый закон Киргхгофа о непрерывности
тока, к точке разветвления 1 (Рис. 9.9).Здесь ![]() -
втекающий в узел ток, вытекающие токи:
-
втекающий в узел ток, вытекающие токи: 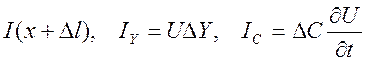 .
Первый закон Кирхгофа:
.
Первый закон Кирхгофа:
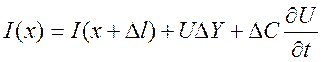 .
.
Разделив
на ![]() , получим второе телеграфное уравнение
, получим второе телеграфное уравнение
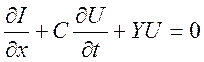 . (9.33)
. (9.33)
Система
телеграфных уравнений (9.32) и (9.33) описывает эволюцию ![]() и
и ![]() в
длинной линии при заданных значениях параметров
в
длинной линии при заданных значениях параметров ![]() . Следует
отметить, что телеграфные уравнения не могут быть получены на основе только
уравнений Максвелла, так как для их получения необходима не содержащаяся в
уравнениях Максвелла информация (сопротивления, емкости и индуктивности длинных
линий). Телеграфные уравнения так же как уравнения Кирхгофа по этой причине
качественно отличаются от уравнений Максвелла.
. Следует
отметить, что телеграфные уравнения не могут быть получены на основе только
уравнений Максвелла, так как для их получения необходима не содержащаяся в
уравнениях Максвелла информация (сопротивления, емкости и индуктивности длинных
линий). Телеграфные уравнения так же как уравнения Кирхгофа по этой причине
качественно отличаются от уравнений Максвелла.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.