Квазистационарные явления в электродинамике. Потенциалы, описывающие квазистационарные поля. Теория цепей, как частный случай квазистационарного приближения, страница 5

                                    .

Электрическое поле, в условиях квазистационарности при отсутствии стороннего тока , удовлетворяет уравнению

                                    ,

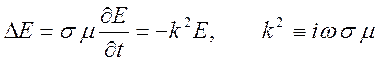которое, благодаря условию 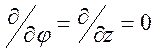, принимает вид

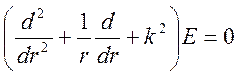                                    .                                                       (9.21)

Это уравнение совпадает с уравнением Бесселя для цилиндрических функций с нулевым значком ():

                                    .

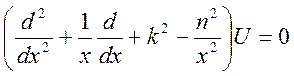Общее решение уравнения (9.21) можно взять в виде

                                    .

Поле  должно быть ограниченным внутри цилиндра и в частности при . Этому условию не удовлетворяет функция Неймана: , значит . Константа  находится из граничного условия при

                                    .

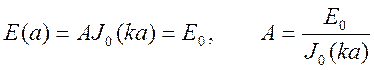В результате получаем

                                    .

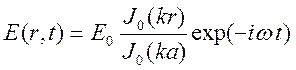Исследуем две предельные ситуации: . Соответствующие разложения для функции Бесселя имеют вид

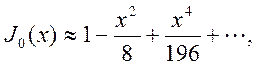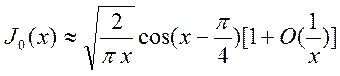                                    при

                                    , при .

Запишем коэффициент  в виде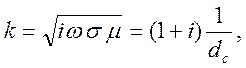

где 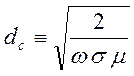 - глубина скин слоя. Условие  соответствует требованию 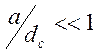, т.е. радиус цилиндра должен быть много меньше глубины скин – слоя. В этом случае , это соответствует приблизительно равномерному распределению поля и плотности тока по сечению цилиндра.

            Более интересен случай ,  - при этом должно быть: 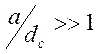 и точка наблюдения не должна приближаться к оси цилиндра. Приближенное представление поля

                                                .

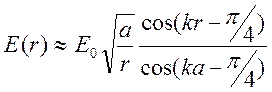Используем представление

     

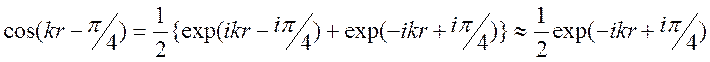
и получим

                                    .

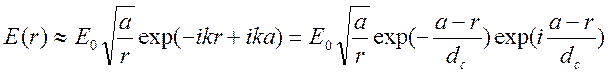Таким образом, при ,  поле и плотность тока по абсолютной величине экспоненциально убывают при удалении точки наблюдения от поверхности цилиндра вглубь проводника. При удалении на глубину скин – слоя  поле уменьшается в  раз.

            При расчете толщины скин – слоя предполагалось, что закон Ома имеет вид , где  - электропроводность при протекании постоянного тока. Такое приближение справедливо только при условии, что поле однородно. Поле не должно изменяться существенно на расстоянии порядка длины свободного пробега  электрона в металле. Это дает ограничение на глубину скин слоя .

            В случае  поле резко неоднородно и наше рассмотрение становится неприемлемым. В этом случае реализуется аномальный скин – эффект. Выполнение условия  можно добиться за счет понижения температуры (увеличивается длина свободного пробега), либо за счет увеличения частоты поля (уменьшается глубина скин - слоя).

            В случае проводника с некруговым сечением точный расчет скин – эффекта представляет значительно более сложную задачу. Требуется одновременное определение поля как внутри так и снаружи проводника. Лишь в предельном случае сильного скин – эффекта задача упрощается, поскольку поле вне проводника может быть определено отдельно используя идеализацию статики и бесконечной электропроводности проводника.

9.6. Движение проводника в магнитном поле. Закон Ома для движущегося проводника. Униполярная индукция.В предыдущем рассмотрении «медленных» процессов использовался закон Ома без учета пространственной и временной дисперсий в локальной форме . Мы уже отмечали одно ограничение на использование такой формы: необходимость достаточно медленного изменения полей. Существует еще одно ограничение: неподвижность проводника относительно системы отсчета, в которой определено электромагнитное поле.

            Рассмотрим ситуацию, когда проводник (или его отдельный участок) движется  со скоростью  относительно системы отсчета , причем , где  - скорость света в вакууме. Такая ситуация называется нерелятивистской. В принципе допустима ситуация, когда  и возможно рассмотрение нелинейной ситуации:. Если перейти в систему отсчета , в которой проводник покоится, то в этой системе можно использовать закон Ома . В разделе 12. «Специальная теория относительности» будет показано, что имеет место преобразование Лоренца, из которого следует