Получим теперь
уравнение для поля ![]() . Для этого применим операцию
. Для этого применим операцию ![]() к уравнению
к уравнению 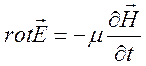 и
учтем, что
и
учтем, что ![]() и имеет место представление
и имеет место представление
![]() .
.
В последнем соотношении
учтено, что ![]() . В результате получим уравнение
параболического типа
. В результате получим уравнение
параболического типа
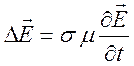 , при
, при![]() .
.
Уравнение такого вида
описывает явление теплопроводности и диффузии, параметр ![]() называется
магнитной вязкостью. Ниже будет показано, что это уравнение не описывает
эффекта запаздывания. Обсудим этот вопрос. Пусть
называется
магнитной вязкостью. Ниже будет показано, что это уравнение не описывает
эффекта запаздывания. Обсудим этот вопрос. Пусть ![]() -
размер системы, протекает процесс,
-
размер системы, протекает процесс, ![]() - длина волны или
характерный пространственный масштаб изменения полей,
- длина волны или
характерный пространственный масштаб изменения полей, 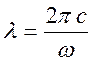 ,
где
,
где ![]() - скорость распространения волны в среде.
Пренебрежение запаздыванием волны в системе возможно при условии
- скорость распространения волны в среде.
Пренебрежение запаздыванием волны в системе возможно при условии ![]() :
:
![]() или
или ![]() ,
,
где ![]() -
время прохождения волны через систему,
-
время прохождения волны через систему, ![]() -
временной масштаб изменения поля.
-
временной масштаб изменения поля.
Для
того, чтобы выяснить основные закономерности диффузии электрического поля,
решим задачу в идеализированной постановке (раздел 9.3). При построении решения
оказывается полезным знание ![]() - теоремы теории
размерности.
- теоремы теории
размерности.
9.2.
![]() - теорема теории размерности. Пусть имеется некоторая зависимость, определяющая
размерную величину
- теорема теории размерности. Пусть имеется некоторая зависимость, определяющая
размерную величину ![]() в виде функции от
в виде функции от ![]() размерных параметров
размерных параметров ![]() :
:
![]() .
.
Если
эта зависимость имеет физическое содержание, то она должна отражать следующий
бесспорный факт. Если определяющие параметры ![]() заданы
в определенной системе единиц измерения, то физическая закономерность
заданы
в определенной системе единиц измерения, то физическая закономерность ![]() , не зависит от произвола при выборе
системы единиц измерения.. Отсюда следуют интересные закономерности. Разобьем
величины
, не зависит от произвола при выборе
системы единиц измерения.. Отсюда следуют интересные закономерности. Разобьем
величины ![]() на две группы. В первую группу
на две группы. В первую группу ![]() включим только определяющие параметры с
независимыми размерностями (например, длина, время и т.д.). Во вторую группу
включим только определяющие параметры с
независимыми размерностями (например, длина, время и т.д.). Во вторую группу ![]() будут входить параметры, размерности
которых можно выразить через размерности величин первой группы. Таким образом,
например, размерность параметра
будут входить параметры, размерности
которых можно выразить через размерности величин первой группы. Таким образом,
например, размерность параметра ![]() имеет вид размерности
произведения параметров первой группы
имеет вид размерности
произведения параметров первой группы
![]() .
.
Размерность
величины ![]() и соответственно размерность функции
и соответственно размерность функции ![]() имеют вид
имеют вид
![]() .
.
Степени
![]() получаются простым подсчетом. Величины
получаются простым подсчетом. Величины
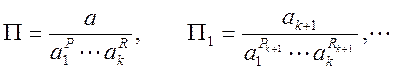
оказываются
безразмерными. Поэтому значения этих величин не зависят от выбора системы
единиц измерения. Независимость закономерности, имеющей физический смысл, от
выбора единиц измерения означает, что соответствующее соотношение ![]() можно представить в виде (это и есть
можно представить в виде (это и есть ![]() - теорема теории размерности):
- теорема теории размерности):
![]() ,
,
где
![]() - безразмерная функция. У этой функции
число аргументов на
- безразмерная функция. У этой функции
число аргументов на ![]() меньше, чем у функции
меньше, чем у функции ![]() .
. ![]() -
теорема явно сформулирована и доказана Э. Бакингамом, хотя ее неявное
использование началось задолго до этого (Фурье, Максвелл, Рейнольдс, Релей)
Рассмотрим два простых примера.
-
теорема явно сформулирована и доказана Э. Бакингамом, хотя ее неявное
использование началось задолго до этого (Фурье, Максвелл, Рейнольдс, Релей)
Рассмотрим два простых примера.
Пример №1 – закон Кулона. Рассмотрим задачу о нахождении потенциала электростатического поля точечного заряда, находящегося в начале сферической системы координат
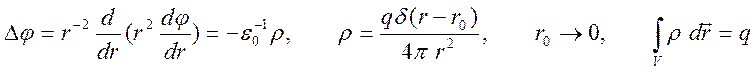 .
.
Необходимость
введения ![]() связана с наличием сингулярности в начале
координат у плотности заряда
связана с наличием сингулярности в начале
координат у плотности заряда ![]() в случае
в случае ![]() .
.
Потенциал
![]() зависит от определяющих параметров
зависит от определяющих параметров ![]() :
:
![]() .
.
В
этой задаче число параметров в обеих группах определяющих параметров одинаково:
![]() . Функция
. Функция ![]() -
безразмерная, величины
-
безразмерная, величины ![]() имеют независимые размерности.
Имеет место соответствие по размерности
имеют независимые размерности.
Имеет место соответствие по размерности
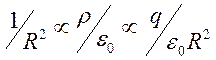
Здесь
значок ![]() обозначает одинаковость размерности.
Согласно
обозначает одинаковость размерности.
Согласно ![]() - теореме имеем
- теореме имеем
![]() .
.
Константа
![]() находится при подстановке этого
представления в неоднородное уравнение Лапласа (с учетом предельного перехода
находится при подстановке этого
представления в неоднородное уравнение Лапласа (с учетом предельного перехода ![]() ):
):
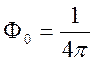 .
.
В результате получаем закон Кулона
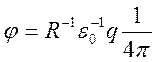 .
.
Пример
№2. Теорема Пифагора. Прямоугольный треугольник целиком и полностью
определяется заданием острого угла ![]() и величины гипотенузы
и величины гипотенузы ![]() . Значит, для площади
. Значит, для площади ![]() имеем представление
имеем представление
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.