Квазистационарные явления в электродинамике. Потенциалы, описывающие квазистационарные поля. Теория цепей, как частный случай квазистационарного приближения, страница 3

                                    .

Опустим перпендикуляр из вершины прямого угла на гипотенузу. При этом основной треугольник разбивается на два подобных ему прямоугольных треугольника: один с площадью , гипотенузой , острым углом  и второй с площадью , гипотенузой , острым углом  (и  это катеты основного треугольника). Площади связаны соотношением . Согласно  - теореме имеем

                                    .

В результате получаем теорему Пифагора

                                                .

            Это доказательство приведено в книге А.Б. Мигдал «Качественные методы в квантовой теории» М. Наука 1975, с. 9-10. Однако, имеется утверждение, что А. Эйнштейн сделал это раньше - в возрасте 11 лет (М. Шредер «Фракталы, хаос, степенные законы», Москва-Ижевск, Регулярная и хаотическая динамика, 2005, стр.25-26)

            Соображения анализа размерностей могут дать содержательный результат. Важнейшим элементом является определение совокупности определяющих параметров. Эта совокупность находится просто, если имеется математическая постановка задачи. В этом случае определяющие параметры - это множество независимых переменных и параметров, входящих в уравнения, граничные, начальные и иные условия, определяющие единственное решение. Правильный выбор определяющих параметров в задаче, не имеющей явной математической формулировки, связан с интуицией исследователя. Успех в этом случае зависит от правильного понимания того, какие параметры важны, а какими параметрами можно пренебречь.

9.3. Диффузия электрического поля. Отсутствие эффекта запаздывания в квазистационарых полях. Рассмотрим решение следующей задачи о диффузии электрического поля. Эволюцию поля опишем уравнением

                                    ,  ,     .

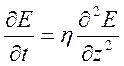Пусть в начальный момент времени  задано условие

                                    .

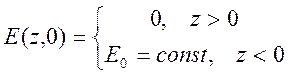Электрическое поле зависит от четырех определяющих параметров

                                                .

Первые три определяющих параметра имеют независимые размерности, а четвертый параметр позволяет составить безразмерную величину

                                                .

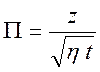Согласно  - теореме поле  будем искать в виде

                                                ,

где  - безразмерная функция. Уравнение в частных производных для поля  приводится к обыкновенному дифференциальному уравнению

                                                .

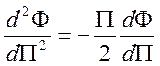Введем вспомогательную функцию 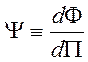, удовлетворяющую уравнению

                                                .

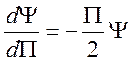Решение этого уравнения имеет вид .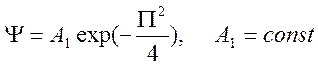

Из определения 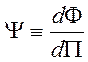 получим

                                    ,

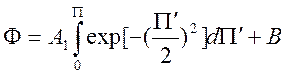или

                                    ,

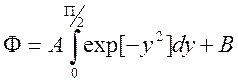где  - произвольные константы, которые находятся из начального условия

                                                .

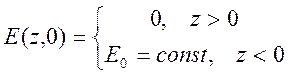При , имеем ,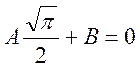

при , имеем ,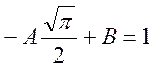

где учтено 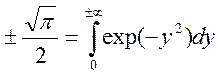. В результате имеем 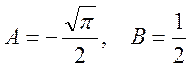. Получаем представление

                                    .

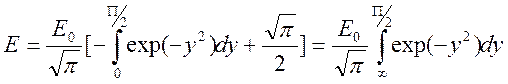Согласно этому представлению  при  - отсутствует эффект запаздывания (возмущения распространяются с бесконечной скоростью). Рассмотрим закономерности перемещения поверхности равной фазы 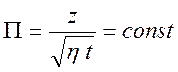, из которого получаем формулу для фазовой скорости 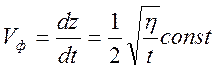 - она конечна, и убывает с увеличением времени. Учет нелинейности  может привести к формированию разрывного поля. Фронт его перемещается с конечной скоростью (реализуется эффект запаздывания).

9.4. Теория цепей.

Расчет электронных схем основан на применении уравнений теории цепей (законы Кирхгофа). Покажем, что эти законы являются следствием квазистационарного приближения для уравнений Максвелла с привлечением дополнительных сведений о цепях (сопротивление, емкость, индуктивность,…)

            Пусть имеем систему линейных токов в замкнутых проводниках. Будем считать, что в каждом контуре  протекает ток

                                    ,

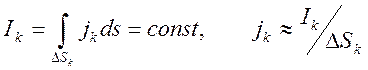где  - площадь поперечного сечения проводника. Вектор плотности тока представим в ви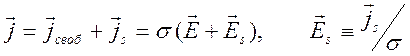де , где  - электропроводность проводника. Циркуляция вектора  по контуру  представляется в виде