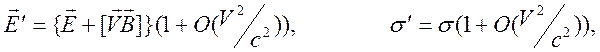
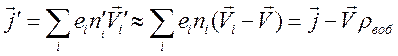
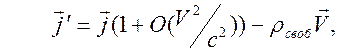
интересуясь
ситуацией слабого нарушения нейтральности (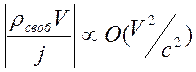 -
подробнее об этом будет сказано в разделе 14.3 – «Обобщенный закон Ома для
медленных нерелятивистских процессов»), будем иметь с точностью до членов
второго порядка малости закон Ома для движущегося проводника
-
подробнее об этом будет сказано в разделе 14.3 – «Обобщенный закон Ома для
медленных нерелятивистских процессов»), будем иметь с точностью до членов
второго порядка малости закон Ома для движущегося проводника
![]() .
.
Таким
образом, в движущемся проводнике сумма ![]() играет
роль «эффективной» напряженности электрического поля, создающей плотность тока
проводимости
играет
роль «эффективной» напряженности электрического поля, создающей плотность тока
проводимости ![]() . Отметим, что обобщенный закон Ома
представляет собой нелинейное соотношение в том случае, когда скорость
. Отметим, что обобщенный закон Ома
представляет собой нелинейное соотношение в том случае, когда скорость ![]() зависит от электромагнитного поля.
зависит от электромагнитного поля.
Диссипация энергии в проводнике при протекании в нем тока не зависит от движения самого проводника. Поэтому плотность джоулева тепла, выделенная за одну секунду, дается формулой
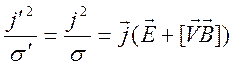 .
.
СоответственноЭ.Д.С.,
действующая в замкнутом линейном контуре ![]() , дается
интегралом
, дается
интегралом
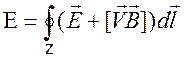 . (9.22)
. (9.22)
Электромагнитное поле в движущихся проводниках в квазистационарном приближении описывается системой уравнений
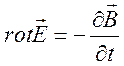 , (9.23)
, (9.23)
![]() , (9.24)
, (9.24)
![]() .
.
Из
уравнения (9.24) (по существу, из закона Ома) имеем 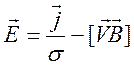 .
Уравнение (9.23) преобразуем
.
Уравнение (9.23) преобразуем
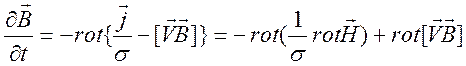 .
.
В однородном проводнике получается уравнение для магнитного поля
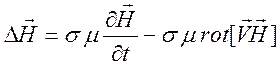 , (9.25)
, (9.25)
где
учтено ![]()
![]() ,
, ![]() .
.
Уравнение
(9.25) это обобщение соответствующего уравнения квазистационарных процессов на
случай движения проводника. Отметим, что такое уравнение будет присутствовать в
разделе 14. «Электродинамика медленных процессов в плазме. Ионно-звуковые
волны. Магнитная гидродинамика», при этом будет ![]() -
скорость движения плазмы. Обсудим относительную роль конвекции (перемещение
электропроводящей среды) и диффузии. Для этого сравним два члена в уравнении
(9.25):
-
скорость движения плазмы. Обсудим относительную роль конвекции (перемещение
электропроводящей среды) и диффузии. Для этого сравним два члена в уравнении
(9.25):
![]() .
.
Это дает неравенство для ситуации преобладания конвекции над диффузией:
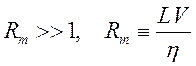 .
.
Здесь
![]() -безразмерное магнитное число Рейнольдса,
-безразмерное магнитное число Рейнольдса,
![]() - пространственный масштаб изменения
полей. Если диффузия преобладает над конвекцией, то неравенство будет
противоположным:
- пространственный масштаб изменения
полей. Если диффузия преобладает над конвекцией, то неравенство будет
противоположным: ![]() .
.
Рассмотрим
эффект униполярной индукции, возникающий при вращении намагниченного
проводника. Неподвижный провод присоединяется к вращающемуся магниту при помощи
двух скользящих контактов А и В (Рис. 9.5). Эффект заключается в создании тока
в этом проводе. Вычислим э.д.с., перейдя в систему координат, вращающуюся
вместе с магнитом с угловой скоростью ![]() . В этой
системе координат магнит неподвижен, а провод вращается с угловой скоростью
. В этой
системе координат магнит неподвижен, а провод вращается с угловой скоростью ![]() . Согласно (9.22), с учетом
. Согласно (9.22), с учетом ![]() , имеем э.д.с.
, имеем э.д.с.
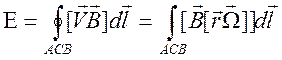 , где
, где ![]() .
.
Эта формула и решает поставленную задачу.
9.7![]() .
Возбуждение тока ускорением. Ускоренное движение металла эквивалентно
появлению дополнительной инерционной силы
.
Возбуждение тока ускорением. Ускоренное движение металла эквивалентно
появлению дополнительной инерционной силы 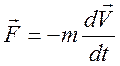 (где
(где ![]() - масса электрона,
- масса электрона, ![]() -
ускорение), действующей на электроны проводимости. Сопоставим этой силе
эквивалентную электрическую силу
-
ускорение), действующей на электроны проводимости. Сопоставим этой силе
эквивалентную электрическую силу ![]() (где
(где ![]() - заряд электрона). Должно быть
- заряд электрона). Должно быть 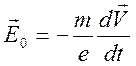 . Таким образом, эффективное электрическое
поле
. Таким образом, эффективное электрическое
поле ![]() , действующее на электроны проводимости в
ускоренно движущемся металле, представляет собой сумму двух полей
, действующее на электроны проводимости в
ускоренно движущемся металле, представляет собой сумму двух полей
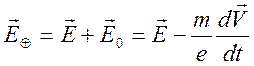 , (9.26)
, (9.26)
где ![]() -
электрическое поле в металле. Закон Ома принимает вид
-
электрическое поле в металле. Закон Ома принимает вид
![]()
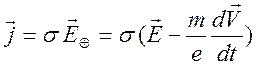 . (9.27)
. (9.27)
Выразим из (9.26) ![]() через
через ![]() и
подставим в уравнение
и
подставим в уравнение 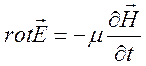 , это дает
, это дает
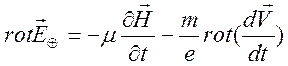 . (9.28)
. (9.28)
Запишем ![]() в
виде суммы двух векторов
в
виде суммы двух векторов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.