Наряду с терминами: «нулевая точка» и «потенциал максимума электрокапиллярной кривой» широко употребляются, как их синонимы, также «потенциал нулевого заряда» и «потенциал незаряженной поверхности», что вносит большую путаницу в электрохимическую литературу. Для того чтобы избежать возможных недоразумений, автор предложил разграничить понятия «нулевая точка» (или «потенциал нулевого заряда») и «потенциал незаряженной поверхности» (или «потенциал максимума электрокапиллярной кривой»), каждому из них присвоить свой символ и употреблять эти термины в соответствии с их содержанием. Основанием для такого разграничения послужили следующие соображения. Потенциал максимума электрокапиллярной кривой ртути (или другого металла) всегда отвечает ее назаряженной поверхности; это значение потенциала целесообразно называть «потенциалом незаряженной поверхности» и обозначать как еq=0. Положение максимума электрокапиллярной кривой и величина отвечающего ему потенциала для данных металла и растворителя меняются в широких пределах в зависимости от природы и концентрации веществ, присутствующих в растворе. В то же время частное значение потенциала незаряженной поверхности, полученное в растворе, не содержащем никаких поверхностно-активных частиц (кроме молекул растворителя) является константой, характерной для данного металла и данного растворителя; это частное значение потенциала незаряженной поверхности целесообразно называть «нулевой точкой» и обозначать как εn. Нулевая точка и потенциал незаряженной поверхности находятся между собой примерно в таком же соотношении, как равновесный и стандартный потенциалы электрода. Последний, как известно, представляет собой частный случай равновесного электродного потенциала εr , который реализуется в растворе с активностями всех участников электродной реакции, равными единице. В обоих случаях необходимо соответствующим образом задать состав раствора, чтобы получить величину, являющуюся характерной константой для данной электродной системы. Допустим, что имеется цепь, составленная из металла, опущенного в раствор его ионов, и стандартного водородного электрода. Э.д.с. этой цепи, равную электродному потенциалу εLM металла Μ в условной водородной шкале, можно записать, в соответствии с уравнением (IX-13), в следующем виде:
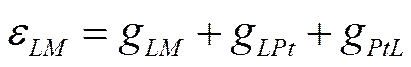
![]()
В свою очередь, гальвани-потенциал на границе раствор—металл, можно представить, согласно уравнению (IX-23), как сумму четырех слагаемых
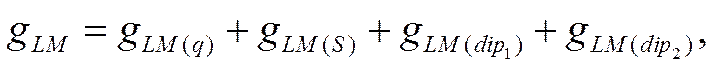
![]()
где индексы q, S, dip1 и dip2 относятся соответственно к потенциал-определяющим ионам, к специфически адсорбирующимся ионам, диполям растворителя и к диполям любого неионизированного органического вещества. Если gLM(q) = 0, то поверхность металла лишена заряда и потенциал электрода должен отвечать потенциалу незаряженной поверхности
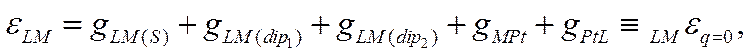
![]()
В согласии со сказанным ранее, потенциал незаряженной поверхности металла зависит от природы этого металла, от примененного электрода сравнения, от природы растворителя и от состава раствора. Для выбранных металла и растворителя величина LMεq=0 может быть различной в зависимости от величины дия(8) (т· е· от природы и концентрации поверхностно-активных ионов) и qLM (dip2) (т.е. от природы и концентрации поверхностно-активных дипольных молекул). Если же, однако, не толькоqLM(q)=0, но и qLM(S) = 0 и qLM (dip)2 = 0. т.е. если в растворе нет никаких поверхностно-активных частиц, кроме молекул растворителя L, то вместо (Х-55) получим
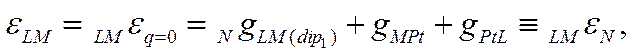
![]()
Как следует из (Х-56), это частное значение потенциала незаряженной поверхности (т. е. нулевая точка LMεN ) должно быть константой, так как оно равно сумме трех постоянных величин.
Нулевую точку можно выразить и через соответствующие вольта-потенциалы
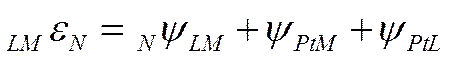
![]()
Вольта-потенциал между металлом и раствором должен быть при этом вполне определенной величиной (NψLM), отвечающей разности внешних потенциалов межу металлом Μ и раствором, в котором потенциал металла равен его нулевой точке.
Определенная таким образом нулевая точка была выбрана за нуль в «приведенной» или «φ-шкале» потенциалов, предложенной автором в 1946—1951 гг. Потенциал φ в приведенной шкале определяется как разность между потенциалом электрода в данных условиях и его нулевой точкой
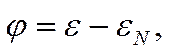
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.