Двойной электрический слой на границе электрод - электролит. Электрокапиллярные явления. Нулевые точки металлов, страница 7

Уравнение, хорошо описывающее форму электрокапиллярных кривых и устанавливающее связь между поверхностным натяже­нием, потенциалом и зарядом на границе ртуть —раствор, было выведено Липпманом

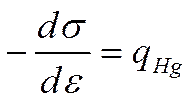
Это уравнение, называемое первым уравнением Липпмана, опре­деляет наклон в любой точке электрокапиллярной кривой, взятый с обратным знаком, как величину, равную удельному заряду q_Hg поверхности ртути при данном значении потенциала ε (по закону электронейтральности заряд поверхности металла должен быть равен заряду раствора у границы раздела, но с обратным знаком, т. е. q_М =-q_L. Следовательно, уравнение (Х-7) позволяет определить также величину заряда той части двойного электрического слоя, которая находится в растворе). В согла­сии с качественной картиной электрокапиллярных явлений, из уравнения (Х-7) следует, что на восходящей ветви кривой q_Hg >0 (dε всегда <0, на восходящей ветви dσ > 0, отсюда dσ/dε < 0 или — dσ/dε > 0), в точке максимума q_Hg = 0 (так как dσ/dε = 0), а на нисходящей ветви q_Hg < 0 ( — dσ/dε < 0). Первое уравнение Липпмана позволяет вычислить по опытным электрокапиллярным кривым величину заряда при любом значении потенциала и построить кривые заряд поверхности ртути — потенциал. Так как заряд поверхности ртути можно измерить непосредственно, имеется воз­можность проверить справедливости формулы Липпмана. Для этого нужно сопоставить расчетные и экспери-ментальные значения заря­да. Подобная проверка была осуществлена Фрумкиным. Получен­ные результаты показали количественную применимость уравнения Липпмана к электрокапиллярным кривым.

Поскольку уравнение (Х-7) определяет величину заряда неза­висимо от его происхождения, оно приложимо к электрокапилляр­ным кривым, полученным в любых растворах, в том числе и в раство­рах, содержащих поверхностно-активные вещества. При одном и том же потенциале, например при потенциале e1 (на рис. 32, а ему отвечает вертикальная пунктирная прямая), и величина, и знак заряда могут быть, в зависимости от природы присутствующих в растворе частиц, различными. В растворе КNОз он отрицатель­ный, в растворе КВ_r — равен нулю, а в растворах KI и K₂S — положительный. Таким образом, анализ электрокапиллярных кри­вых, так же как и данные, полученные при изучении электрокине­тических явлений, указывают на возможность перезарядки поверхности металла в присутствии поверхностно-активных веществ при сохранении неизменной общей величины скачка потенциала между металлом и раствором.

Известно, что производная от заряда по потенциалу дает диф­ференциальную емкость C_d, т. е. величину, характеризующую изменение заряда с потенциалом

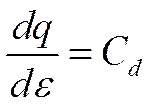
Величину дифференциальной емкости можно найти также с по­мощью электрокапиллярных кривых. Действительно, из уравне­ний (Х-7) и (Х-8) следует, что

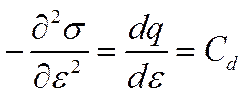
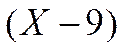
Выражение (X-9) известно как второе уравнение Липпмана. Уравнение (Х-8) можно представить в следующем виде:

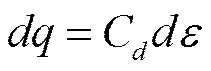
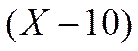
Так как в точке максимума электрокапиллярной кривой q = О, а ε = ε_3ΚΜ, то, проинтегрировав (Х-10),

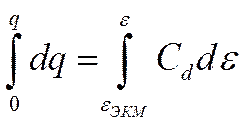
получим

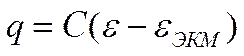
или

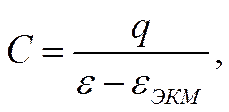
где С — интегральная емкость при потенциале ε. На рис. 34 при­ведены электрокапиллярная кривая и соответствующие ей кривые: заряд металл — потенциал и дифференциальная емкость — потенциал,

­

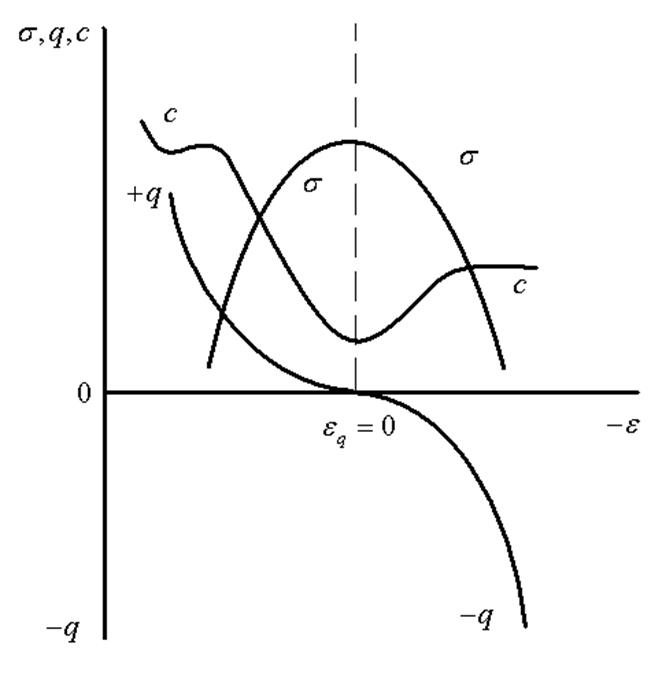
Типичные кривые: поверхностное натяжение () – потенциал (); заряд поверхности (q) – потенциал (); ёмкость двойного слоя (С) – потенциал () на границе раздела ртуть – раствор поверхностно-инактивного электролита.