Двойной электрический слой на границе электрод - электролит. Электрокапиллярные явления. Нулевые точки металлов, страница 10

Обе величины, входящие в правую часть уравнения (Х-58), должны быть, естественно, выражены в одной и той же условной, например, в водородной шкале; величина φ-потенциала при этом не зависит от выбранной условной шкалы.

Поскольку для различных металлов величины ε_Ν не совпадают, (см. табл. 40—41), то у каждого металла должна быть своя собствен­ная приведенная шкала, основанная на его нулевой точке. Приведен­ная или φ-шкала потенциалов отличается, таким образом, и от любой условной, и от абсолютной шкалы потенциалов. Это разли­чие отчетливо проявляется при сопоставлении значений стандарт­ных электродных потенциалов ряда металлов в водородной, абсо­лютной и приведенной шкалах (табл. 39).

Из табл. 39 следует, что в водородной и абсолютной шкалах порядок расположения металлов по возрастающему положитель-

                                                                                                                                             Таблица 39.

Стандартные потенциалы некоторых металлов в различных шкалах, в

* За нулевую точку железа принята не —0,38 β (см. табл.  37),   а  более вероятная величина, равная нулю.

** За нулевую точку серебра принята не табличная величина —0,76 в, а более вероят­ная, равная —0,4 в.

ному значению стандартного электродного потенциала, а также разности потенциалов между двумя любыми электродными потен­циалами остаются одними и теми же. В приведенной шкале потен­циалов порядок расположения металлов и разности в величинах их стандартных электродных потенциалов совершенно иные, так как физический смысл величины потенциала в любой условной (и абсолютной) шкале и в приведенной шкале совершенно различен. В то время как условная шкала относит величины потенциалов к одному определенному электроду, потенциал которого принят за нуль, в приведенной шкале для каждого электрода потенциал отсчитывается от своего собственного нуля, равного нулевой точке этого металла. Неверно поэтому применять φ-шкалу потенциалов для решения проблем, связанных с термодинамикой электрохими­ческих систем или с электродным равновесием и пытаться исполь­зовать ее вместо водородной шкалы или ε-шкалы потенциалов. Приведенная шкала не позволяет, например, определить направле­ние реакции и величину э.д.с. равновесной электрохимической системы, составленной из двух электродов с известными значениями φ-потенциалов. Эту задачу легко решить при помощи ε-шкалы. Однако потенциал в ε-шкале не дает сведений ни о заряде поверх­ности металла, ни о структуре двойного электрического слоя, ни о том, какова наиболее вероятная электрическая природа тех частиц, которые при данных условиях должны преимущественно адсор­бироваться на поверхности электрода. Эти (и другие) сведения осо­бенно важны для понимания неравновесных электродных процес­сов и их можно получить, пользуясь φ-шкалой протенциалов. Исходя из определения φ-потенциала (Х-58) и учитывая, что потенциал ε, отличный от потенциала ε_n, дается уравнением

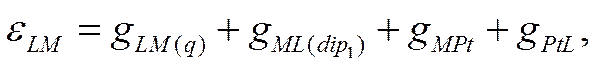
получим следующее выражение для потенциала электрода в φ-шкале:

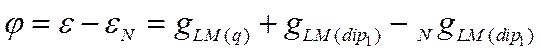
Уравнение (X-60) позволяет рассматривать потенциал электрода в φ-шкале как меру заряда металла (интенсивности ионного двой­ного слоя q_LM(q)) и как меру изменения ориентации полярных молекул растворителя на границе металл — электролит при пере­ходе от нулевой точки к данному значению потенциала (разность величин q_LM(dip1) и _Nq_LM(dip1)· Полагают, что ориентация дипо­лей растворителя на незаряженной поверхности металла мало зависит от его природы и для всех металлов в водных растворах _Nq_LM(dip1) примерно одно и то же. Таким образом, если, например, для металла 1 и металла 2

φ₁=φ₂

__________________________

*  Уравнения (Х-59) и (Х-60) относятся  к растворам,  не содержащим поверхностно-активных  веществ  (g_LM(s) ⁼ 0)·