Двойной электрический слой на границе электрод - электролит. Электрокапиллярные явления. Нулевые точки металлов, страница 2

Изучение связи, существующей между направлением и скоро­стью электрофореза или электроосмоса, с одной стороны, и направ­лением и напряженностью приложенного электрического поля, с другой, позволяет получить сведения о знаке и величине заряда твердых частиц относительно жидкости и о соответствующем ему скачке потенциала.

Приближенная теория электрокинетических явлений приводит к следующим уравнениям для скорости электроосмоса U и вели­чины потенциала течения (или седиментации) Ε

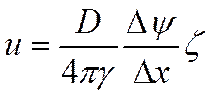
и

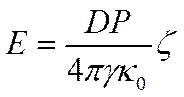
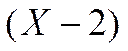
где D — диэлектрическая постоянная жидкой фазы;  Δψ/Δx— напряженность электрического поля в направлении, параллельном гра­нице раздела твердой и жидкой фаз; γ — вязкость жидкой фазы; k₀ —ее удельная электропроводность; Ρ —давление, вызывающее относительное перемещение фаз по границе раздела между ними; Ω —сечение взвешенной частицы (или поры). В случае электро­фореза

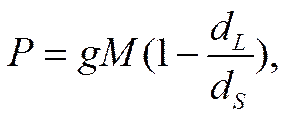
где g — ускорение силы тяжести; Μ — масса взвешенных частиц, проходящих через 1 см³ сечения микрогетерогенной системы, a d_L и d_s — плотность жидкости и взвешенных твердых частиц, соот­ветственно.

Величина ζ, входящая в уравнения (Χ-Ι) и (Х-2), называется «дзета-потенциалом» или «электрокинетическим потенциалом»; его можно найти с помощью уравнений (Х-1) и (Х-2), если измерить U или Е. Необходимо, однако, иметь в виду, что уравнения (Х-1) и (Х-2) в силу их приближенности позволяют определить ориенти­ровочные значения ζ-потенциала Непосредственные измерения дают при этом не ζ,, а Dζ/γ, и расчетная величина ζ-потенциала зави­сит от выбора численных значений D и γ.

    В уравнения (Х-1) или (Х-2) подставляют значения диэлектрической постоянной и вязкости жидкой фазы, которые могут не совпадать с диэлектрической постоянной и вязкостью жидкости непосредственно у границы раздела. Рассчитанные по этим уравнениям ζ-потенциалы могут поэтому заметно отличаться от их истинных значений. Помимо того, напряженность поля и удельная электропроводность жидкости вблизи границы раздела т. е. величины, которые следовало бы использовать при расчете ζ-потенциала по уравнениям (Х-1) и (Х-2)] и в глубине жидкой фазы в общем случае не совпадают. Такое различие обусловлено тем, что у поверхности раздела фаз ионный состав обычно иной, чем средний ионный состав всей жидкой фазы Это находит свое отражение в появлении так называемой поверх­ностной проводимости k' Как показал Бикерман в результате появления поверхностной проводимости напряженность поля вблизи границы раздела (Δψ/Δx)_LS   обычно меньше,   чем средняя макроскопическая напряженность поля, причем

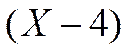
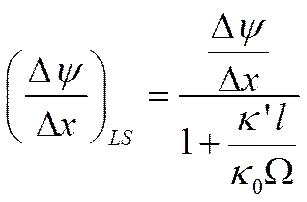
если l — периметр поры или частицы.

Считалось, что ζ-потенциал коллоидной химии—это то же самое, что электродный потенциал или ε-потенциал электрохимии; точнее та его часть, которая отвечает скачку потенциала на границе электрод —электролит. Для такого предположения имелись изве­стные основания, вытекающие из самой природы электрокинети­ческих явлений.

Действительно, если граница раздела жидкость — твердое тело в то же время является плоскостью скольжения при относительном перемещении фаз, то ζ-потенциал должен быть равен ε-потенциалу или, вернее, скачку потенциала g_LM. Если бы это предположение оказалось справедливым и отвечающим опыту, то появилась бы возможность экспериментального измерения скачка потенциала электрод — электролит, а следовательно, и определения абсолютного потенциала электрода.

Проверить справедливость этого предположения прямым сравнением независимо найденных значе­ний ξ-потенциала и g_LM-потенциала невозможно, так как гальвани-потенциал g_LM не может быть определен экспериментально. Однако имеется возможность косвенной проверки сопоставлением зависи­мости ζ-потенциала и ε-потенциала от состава раствора.