Расчет на прочность крышки под постоянным внутренним давлением с помощью расчетного пакета ANSYS. Расчет на изгиб вала с помощью расчетного пакета ANSYS

БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ВОЕНМЕХ» имени Д.Ф. Устинова

────────────────────────────────────

КАФЕДРА МЕХАНИКИ ДЕФОРМИРУЕМОГО

 ТВЕРДОГО ТЕЛА

КУРСОВАЯ РАБОТА

Тема: «Длительная усталость»

Преподаватель: Санников В.А.

Студент: Бертова А.В. 

Группа: К-301

Санкт-Петербург

2004г.

Часть I. Расчет на прочность крышки под постоянным внутренним давлением с помощью расчетного пакета ANSYS

Схема расчет на прочность данного объекта с необходимыми пояснениями

1. Изучение эскиза и трехмерной модели (см. чертеж и рис. 1) и построение геометрической модели в ANSYS (рис. 3).
2. Создание конечномерной сетки и наложение ее на объект (рис. 4). В данном случае был использован элемент высокого порядка – квадратичный криволинейный треугольный элемент содержащий шесть узлов PLANE 2(рис. 2).. Это обусловлено тем что при применении таких элементов сокращается время обработки данных в сочетании с высокой точностью расчетов

Рис. 1. Трехмерная модель крышки	Рис. 2.  PLANE 2.

3. Учет закреплений (рис 5). Закрепляем с торца, в радиальном направлении и во фланце по вертикали.
4. Приложение внутреннего давления (рис. 6).
5. Решение: в упругой области (рис. 7, 8, 9, 10, 11, 12, 13).
6. Добавление в свойства материала параметров характеризующих пластическое состояние и решение уже в этой области (рис. 14, 15, 16)

Рис 3. геометрическая модель заданной крышки	Рис. 4. Создание конечномерной сетки и наложение ее на исследуемый объект

Рис. 5. Учет закреплений (симметрия и фланец)	Рис. 6. Приложение внутреннего давления

Вывод узловых результатов для упругой области

Рис. 7. Меридиональные напряжения
Рис. 8. Окружные напряжения
Рис. 9. Третья гипотеза прочности (максимальные касательные напряжения)
SINT   SY   SZ
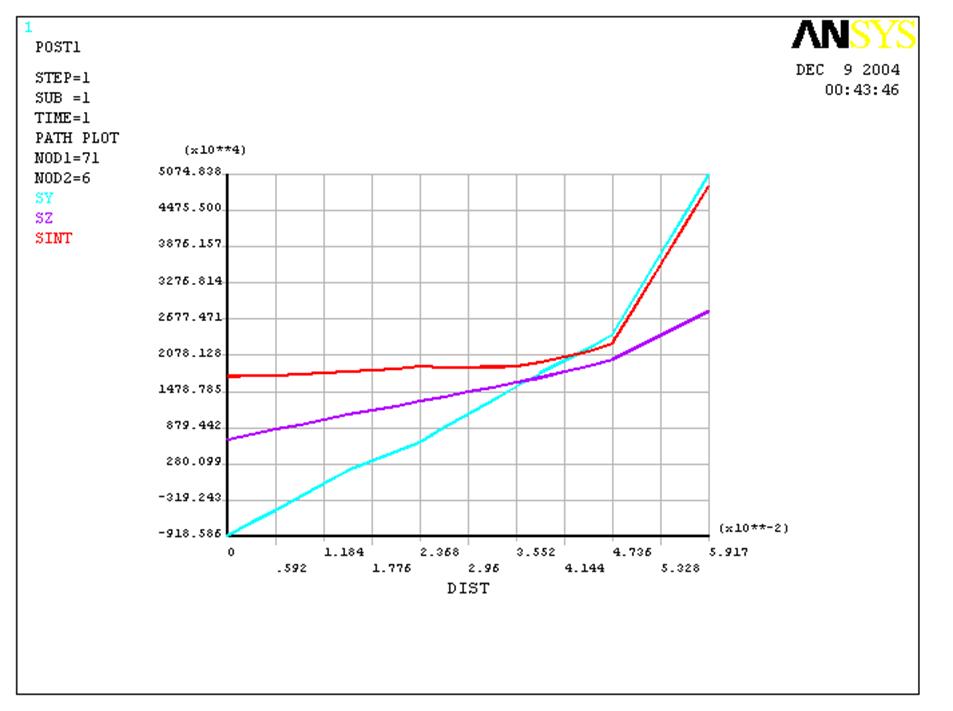
Рис. 10. График компонент напряжений в сечении вблизи фланца
Рис. 11. Эпюра изменения меридионального напряжения	Рис. 12. Эпюра изменения окружного напряжения
Рис. 13.Эпюра изменения напряжений, определенных по третьей гипотезе прочности

Вывод узловых результатов для пластической области

Рис. 14. Изменение меридиональных напряжений

Рис. 15. Изменение окружных напряжений

Рис. 16. Третья гипотеза прочности (максимальные касательные напряжения

Теоретическое решение

1.  Определение напряжений по безмоментной теории

Рассмотрим крышку как коническую оболочку толщиной , Через  обозначен радиус дуги меридиана срединной поверхности. Через  обозначен радиус кривизны нормального сечения, перпендикулярного к дуге меридиана, равен отрезку заключенному между срединной поверхностью и осью симметрии.  и  являются функциями угла  - угла между нормалью и осью симметрии (рис. 17).

Рис. 17.	Рис. 18.

Рис. 19.

            Двумя парами меридиональных и нормальных конических сечений выделим элемент (рис. 18.) на гранях элемента возникают меридиональные  и окружные  напряжения, умноженные на соответствующие площади граней элемента , они дадут силы  и  (рис. .19). Также на элемент действует сила нормального давления .

            Проецируя на нормаль, получаем:

В итоге получаем уравнение Лапласа:

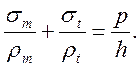
            Проецируя силы на направление оси оболочки можно составить еще одно уравнение:

             где Р осевая равнодействующая всех сил.

            В данном случае:

           

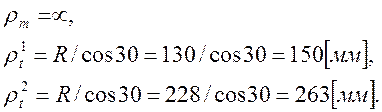
            Осевая составляющая:                   

            Меридиональное напряжение: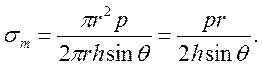      

            Окружное напряжение: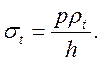                  

            В данном случае:     

                                              

                                              

                                                                                                                                  Таблица 1

Сводная таблица значений напряжений

Рис. 20.	Рис. 21.

2.  Определение напряжений при действии в оболочке изгибающих моментов и нормальных сил

Упростим задачу следующим допущением, вместо конуса рассматриваем цилиндр. Определяем напряжения в окрестности фланца.

С читаем, что осевая растягивающая сила Т_х=0, так как давление р от  высоты крышки не зависит, то частное решения уравнения: