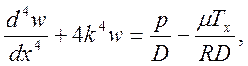Расчет на прочность крышки под постоянным внутренним давлением с помощью расчетного пакета ANSYS. Расчет на изгиб вала с помощью расчетного пакета ANSYS, страница 2

 имеет вид:

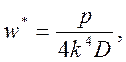 где 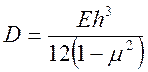 – жесткость пластины (оболочки) на изгиб.

Суммарное решение выше указанного уравнения:

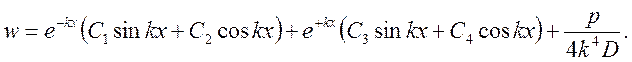
Второе слагаемое  неограниченно возрастает с увеличением высоты цилиндра, а величина перемещения w должна быть постоянной при достаточно большой высоте, следовательно чтобы не возникало противоречий положим:

Постоянные С₁ и С₂ подберем так, чтобы в начале отсчета х, т.е. в месте сопряжения цилиндра с жестким фланцем, перемещение w и угол поворота dw/dx jобращались бы в ноль. Получаем:

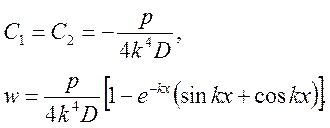
При достаточно большом значении высоты крышки функция w принимает значение:

Для цилиндра влияние краевого эффекта распространяется на участок длиной:

.

3.  Расчет меридиональных напряжений

Максимальный изгибающий момент М_х:, вблизи фланца

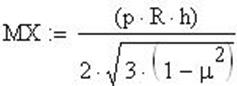
Расчет меридиональных напряжений и построение графика:

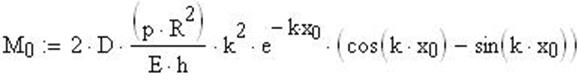
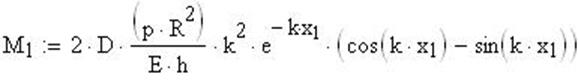
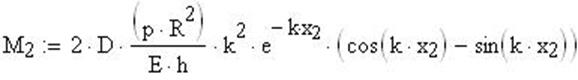
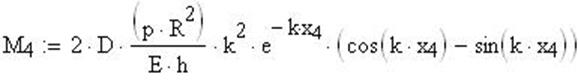
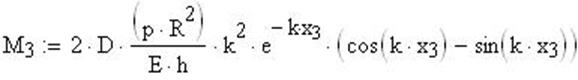
Напряжение с учетом расчетов по безмоментной теории:

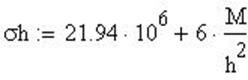
Вектор столбец напряжений:

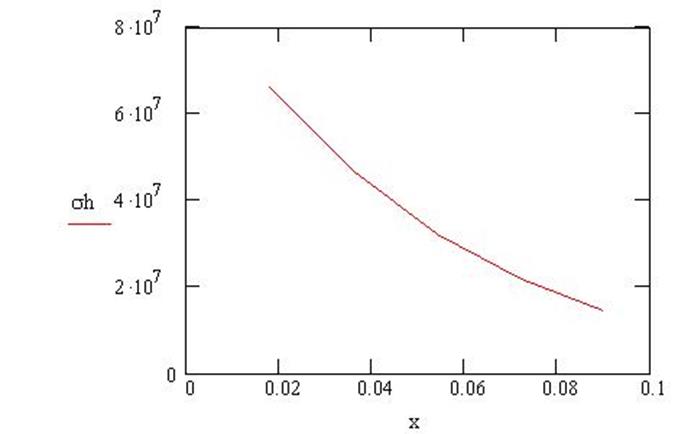
Рис.22. График изменения меридиональных напряжений по высоте

Напряжение для сечения, лежащего выше фланца на высоте равной 0,0173м

           

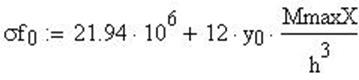
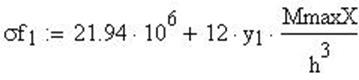
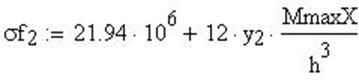
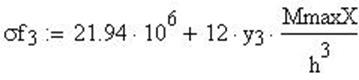
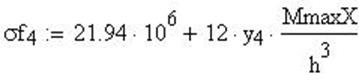
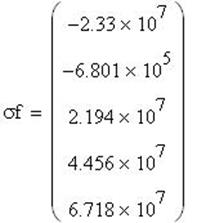
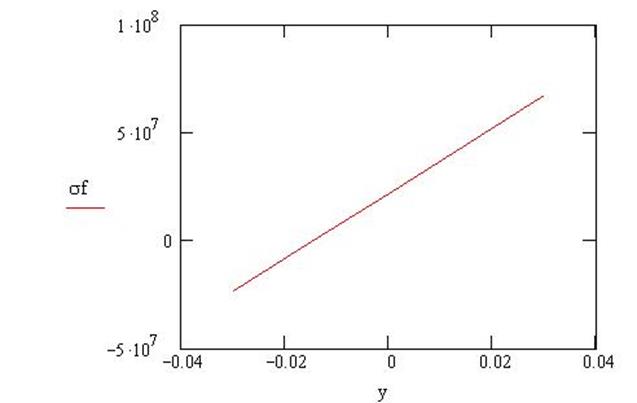
Рис.23. График изменения меридиональных напряжений по ширине сечения

4.  Расчет окружных напряжений

Максимальный изгибающий момент М_х:, вблизи фланца:

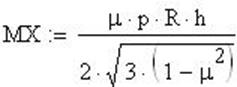
Расчет меридиональных напряжений и построение графика:

Напряжение с учетом расчетов по безмоментной теории:

 

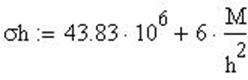
Вектор столбец напряжений:

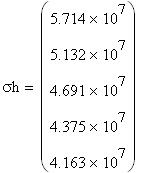
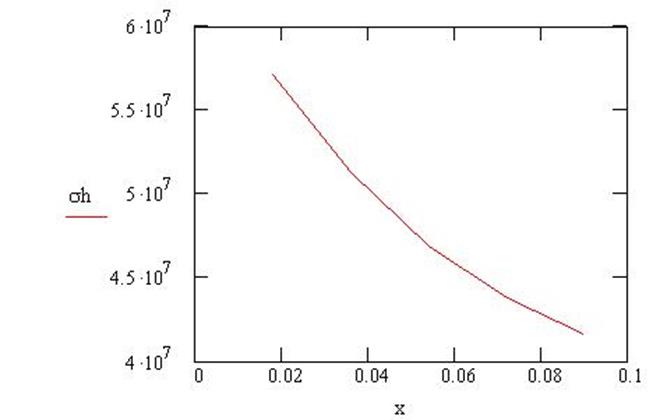
Рис.24. График изменения окружных напряжений по высоте

Напряжение для сечения, лежащего выше фланца на высоте равной 0,0173м

           

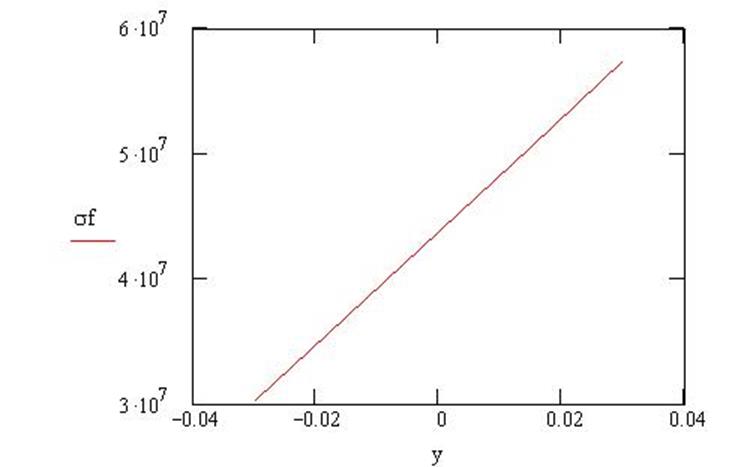
            Рис.25. График изменения окружных напряжений по ширине сечения

Часть II. Расчет на изгиб вала с помощью расчетного пакета ANSYS

Схема расчета данного объекта с необходимыми пояснениями

1.  Изучение схемы вала (рис. 26).

2.  Построение геометрической модели в ANSYS было начато с точек на рабочем пространстве, затем были проведены линии и сделано скругление (рис. 28). Потом задана поверхность (рис. 29)

3.  Создание конечномерной сетки и наложение ее на объект (рис. 27). В данном случае был использован элемент высокого порядка – квадратичный криволинейный четырехугольный элемент содержащий четыре узла PLANE 42. Это обусловлено тем что при применении таких элементов сокращается время обработки данных в сочетании с высокой точностью расчетов. Далее вращением вокруг оси получаем объемное тело уже покрытое конечномерной сеткой элементов (рис. 30).

Рис. 26. Схема вала	Рис. 27. PLANE 42

4.  Учет закреплений (рис 31). Закрепляем по OY по нижней половине вала в двух местах и поOX в точке, в одном из закреплений.

5.  Приложение внешнего давления по поверхности (рис. 32).

6.  Решение: в упругой области, просмотр результатов- распределения осевых напряжений во всем валу и по его сечению вблизи концентратора (рис. 33 и 34).

Рис. 28.	Рис. 29

Рис. 30.

Рис. 31.

Рис. 32.

Рис. 33

Рис. 34

Рис. 35

Рис. 36

Распределение напряжений при более густом разбиении

Рис. 37

Рис. 38

Рис. 39

Рис. 40

Рис. 41.

Теоретическое решение

1.  Понятие об усталостном разрушении материала и его причины

Многие детали машин и элементы сооружений в процессе эксплуатации подвергаются действию нагрузок, меняющихся во времени. Если уровень напряжений, вызванных этими нагрузками, превышает определенный предел, то в материале начинают происходить необратимые процессы накопления повреждений, которые приводят к образованию трещины. В свою очередь, концентрация напряжений на краю трещины способствует дальнейшему ее развитию.