Расчет на прочность крышки под постоянным внутренним давлением с помощью расчетного пакета ANSYS. Расчет на изгиб вала с помощью расчетного пакета ANSYS, страница 6

Первый способ заключается в том, что всю партию образцов разбивают на несколько серий. Для каждой серии устанавливают среднее значение напряжения σ_m. В результате испытаний определяют максимальное значение σ_а, под которым понимается наибольшее значение амплитуды, не вызывающее разрушения образца до базы испытаний при заданном среднем напряжении σ_m. Полученные таким образом напряжения σ_m и σ_а определяют на диаграмме предельных амплитуд одну точку. По результатам испытаний всех серий образцов находят несколько точек указанной диаграммы.

При втором способе для каждой серии образцов сохраняется постоянным коэффициент асимметрии цикла ρ (при переходе от образца к образцу σ_m и σ_а изменяются, но так, что величина ρ остается постоянной). Предельная амплитуда, в данном случае, это наибольшее значение напряжения, которое при заданном коэффициенте асимметрии не вызывает разрушения образца до базы испытаний.

Назначение диаграммы предельных амплитуд состоит в следующем: допустим, что цикл нагружения образца характеризуется параметрами σ_m,σ_а Если точка, отвечающая этим значениям (Тд, ст^, оказывается ниже кривой Са~0т на рис. 53, то рассматриваемый образец способен выдержать неограниченное число циклов или по крайней мере не разрушится до базового числа Ne. Если же точка оказалась выше указанной кривой, то образец разрушится при каком-то ограниченном числе циклов или при числе циклов, меньшем базового числа.

Построение диаграмм предельных амплитуд трудоемкая задача, в связи с этим часто идут по пути ее схематизации (рис. 54). Верхняя часть кривой заменяется прямой, проходящей через две точки А и В, причем точка А соответствует симметричному циклу, а точка В — пульсационному (отнулевому) циклу. Прямая AD описывается уравнением:

 или  где                                                                    (2)

.

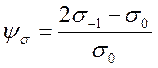Если материал является хрупким, то правая часть диаграммы заменяется прямой, наклоненной к оси  под углом 45° и проходящей через точку С, соответствующую пределу прочности материала при постоянном во времени нагружении. Для точек этой прямой справедливо равенство , из которого следует, что максимальное напряжение не должно превосходить предела прочности материала. Если материал обладает пластическими свойствами, то абсцисса С выбирается равной пределу текучести материала σ_т. В некоторых случаях для хрупких материалов диаграмма предельных амплитуд схематизируется одной прямой, проходящей через точки А (0, σ_-1) и С (σ_в, 0) (рис. 54). Уравнение прямой АС по виду совпадает с уравнением (2), но с коэффициентом

5.  Факторы, влияющие на усталостную прочность материала

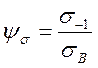
На предел выносливости материала оказывают влияние многие факторы. Рассмотрим влияние каждого из них в отдельности.

Концентрация напряжений. Концентрация напряжений при циклическом изменении нагрузки вызывает в зоне очага концентрации зарождение и последующий рост трещины, который завершается усталостным разрушением. Для учета влияния концентрации напряжений на предел выносливости вводится эффективный коэффициент концентрации напряжении k_σ, равный отношению предела выносливости «гладкого» образца σ_ρ и образца с концентратором напряжений σ_ρk , т. е..

Экспериментально установлено, что коэффициент β уменьшается с увеличением коэффициента асимметрии цикла, т. е. по мере приближения нагружения к статическому, поскольку местные напряжения оказываю г малое влияние на статическую прочность материала.

Хотя коэффициент β должен определяться для каждого значения коэффициента асимметрии цикла, вследствие недостаточности экспериментальных данных в расчетах обычно используются числовые значения эффективного коэффициента концентрации напряжений для симметричного цикла:.

Влияние концентрации напряжений на предел выносливости иногда учитывается коэффициентом чувствительности материала к местным напряжениям:

 где  – теоретический коэффициент концентрации напряжений.

Коэффициент q зависит главным образом от свойств материала. Для конструкционных сталей коэффициент q≈0,6...0,8, причем более прочным сталям соответствуют большие значения q. Поэтому применение высокопрочных материалов при переменных нагрузках не всегда целесообразно.