Рассмотрим схематизированную диаграмму деформирования материала, показанную на рис. 60, а. Рядом (рис. 60, б) приведен график изменения напряжений во времени. При первом нагружении вдоль кривой ОАВ точка, изображающая состояние материала, движется вдоль диаграммы деформирования по линии ОАВ. Затем напряжения уменьшаются и та же точка движется по линии ВВ1А1. По достижении напряжением минимального значения начинается его возрастание и деформирование совершается далее по замкнутой линии А1АВВ1.
|
|
|
Рис. 60. Схематизированная диаграмма деформирования материала (а) и график изменения напряжения во времени (б) |
Размах
деформаций за один цикл равен 
, а размах пластических
деформаций
, где εпл
max ,εпл min – максимальная и минимальная пластические
деформации при циклическом изменении напряжений. Характер разрушения при
малоцикловой усталости зависит от способности материала к накоплению
пластических деформаций при циклическом деформировании. Материалы называются
циклически стабильными, если остаточная деформация не меняется во всех циклах. Рассмотренный
выше пример иллюстрирует особенности деформирования таких материалов.
Для циклически разупрочняющихся материалов характерны увеличение остаточных деформаций и рост суммарной пластической деформации.
Если остаточная деформация уменьшается от цикла к циклу, а суммарная пластическая деформация стремится к некоторому предельному значению, то такой материал называется циклически упрочняющимся.
Расчет на малоцикловую прочность связан с большими трудностями, которые в значительной степени объясняются недостатком экспериментальных данных. В некоторых случаях единственным выходом из этого положения является проведение испытаний натурных узлов или их моделей.
Одним из способов повышения сопротивления элементов конструкций малоцикловому усталостному разрушению является изготовление их из циклически упрочняющихся материалов.
10. Решение поставленной задачи
|
|
|
Рис. 54. |
Уравнения равновесия:
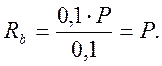
Моменты сопротивления для меньшего и большего сечения, соответственно:
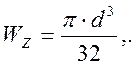
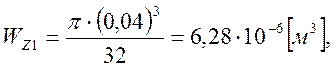
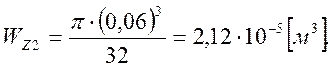
Уравнения моментов:
Напряжения возникающие в сечениях, соответственно:
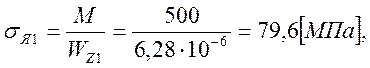
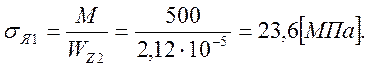
Учет основных факторов, влияющих на предел выносливости материала вала при переменном изгибе. В сечении имеется концентратор в виде галтели:
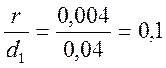
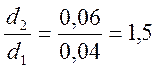
Эффективный коэффициент напряжений для ступенчатых валов при изгибе:
(рис. 18.12, стр. 272, [3])
Поправочный коэффициент
(рис. 18.14, стр. 272, [3])
Эффективный коэффициент концентрации:
Масштабный коэффициент
(рис. 18.11, стр. 272, [3])
Под действием изгибающего момента вследствие вращения вала нормальные напряжения будут меняться по симметричному циклу.
Отсюда получим выражение для коэффициента запаса по усталости ой прочности конструкции:
,
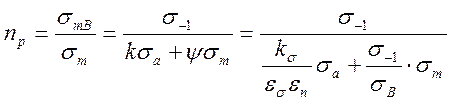- предел выносливости,
- временное сопротивление материала вала
при растяжении,
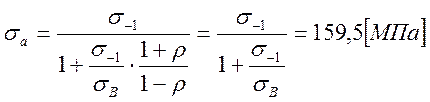- амплитуда цикла,
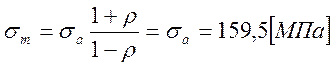- среднее напряжение цикла,
- эффективный коэффициент концентрации,
-коэффициент учета состояния поверхности
(для полированного вала 
)
- Масштабный коэффициент
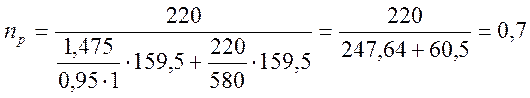
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Сопротивление материалов: Учеб. для вузов. – Высш. шк., 1995. – 560 с.: ил.
Кинетический теории механической усталости и ее приложения. Минск. «Наука и техника», 1973, стр. 216.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
