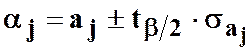Методичні вказівки до контрольної роботи з дисципліни "Економетрія", страница 9

,

де 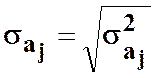 - стандартна помилка оцінки параметра .

Якщо модель адекватна, то можна знаходити прогнозні значення залежної змінної увиходячи з побудованої моделі. При цьому можна отримувати два типи прогнозів: точкові та інтервальні. Точковий прогноз дає значення залежної змінної, наприклад,  для відповідного значення  з побудованої вибіркової моделі:

.

При цьому, виходячи з узагальненої моделі, дійсне значення у для відповідного значення  буде дорівнювати:

,

де  - значення випадкової величини, не спостережуваної для значення . Дійсне значення  знайти неможливо, можна лише оцінити його за допомогою прогнозу.

Отже, прогнозне значення  є оцінкою дійсного значення змінної . Таким чином, з вибіркової моделі легко можна знаходити будь-яке прогнозне значення. Зазначимо, що таке прогнозне значення буде точковим. Виходячи з отриманого точкового прогнозу можна побудувати інтервали довіри для дійсного значення залежної змінної. Такий інтервал довіри при заданому рівні значущості  для  буде знаходитись за формулою:

.

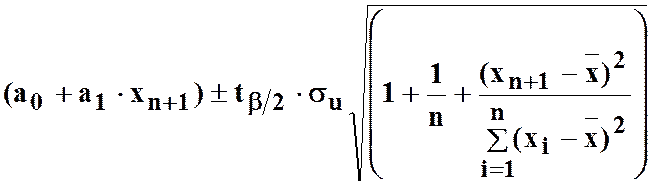Ця формула дає інтервал довіри для дійсного окремого значення залежної змінної.

На практиці більш важлива побудова інтервалів довіри для математичного сподівання . В цьому разі формула дещо модифікується і має вигляд:

.

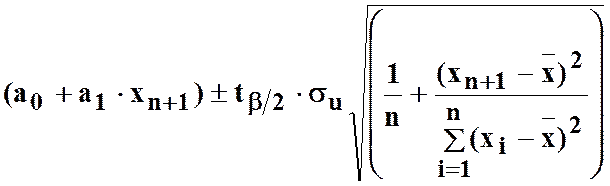Приклад виконання завдання 3

Завдання 3 виконується за результатами завдання 2 з використанням розрахункових таблиць 9 і 10 для вибіркової економетричної моделі:

.

Для перевірки статистичної значущості параметрів вибіркової регресії a₀ і a₁ розрахуємо оцінку дисперсії залишків:

 ;   ;

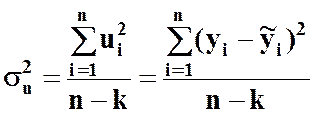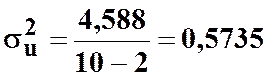А також оцінки дисперсій параметрів регресії:

 ;   .

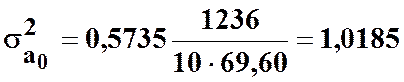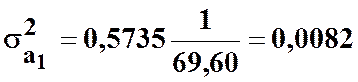Розрахуємо t-статистику для параметра a₀

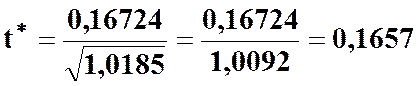
 і параметра a ₁

.

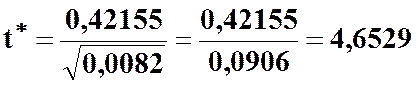Задаємо рівень значущості  (5%). Оскільки кількість спостережень 10, то кількість ступенів свободи відповідно дорівнює 8. За таблицею 12 розподілу Ст’юдента знаходимо 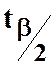 критичне значення з 8 ступенями свободи. Воно дорівнює .

Для параметра a ₀ отримаємо , тобто t^* потрапляє не в критичну зону і можна стверджувати, що з ймовірністю 0,95 оцінка параметра a₀ є статистично незначущою. Тому приймається гіпотеза про .

Для параметра a₁ отримаємо, що t^* потрапляє в критичну зону і можна стверджувати, що з ймовірністю 0,95 оцінка параметра a₁ є статистично значущою. Тому приймається гіпотеза про .

Побудуємо інтервали довіри для параметрів узагальненої регресійної моделі:

або .

або .

Тобто підтверджується гіпотеза про статистичну незначущість параметра , оскільки інтервал довіри для цього параметра включає нульове значення і треба оцінювати параметр моделі . Оскільки модель адекватна, то можна знаходити прогнозні значення, наприклад, для =16. Точковий прогноз дорівнює:

.

Виходячи з отриманого точкового прогнозу, побудуємо інтервал довіри для дійсного значення у:

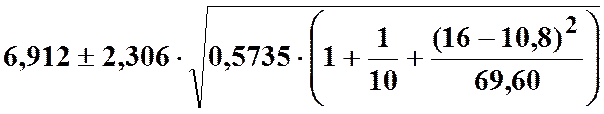 або .

Тобто    з ймовірністю 0,95.

Для математичного сподівання  інтервал довіри дорівнює

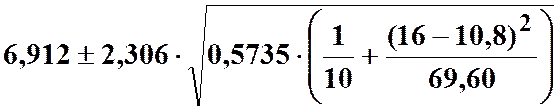 або .

          Тобто з ймовірністю 0,95   .

Таблиця 12 – Розподіл Ст’юдента  ()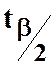

	або
	0,10	0,05	0,025	0,01	0,005
	0,20	0,10	0,050	0,02	0,010
1	3,078	6,314	12,706	31,821	63,657
2	1,886	2,920	4,303	6,965	9,925
3	1,638	2,353	3,182	4,541	5,841
4	1,533	2,132	2,776	3,747	4,604
5	1,476	2,015	2,571	3,365	4,032
6	1,440	1,943	2,227	3,143	3,707
7	1,415	1,895	2,365	2,998	3,499
8	1,397	1,860	2,306	2,896	3,355
9	1,383	1,833	2,262	2,821	3,250
10	1,372	1,812	2,228	2,764	3,169