Методичні вказівки до контрольної роботи з дисципліни "Економетрія", страница 7

Номер спостереження	Вартість основних фондів (хі), млн. грн	Випуск продукції (уі), млн. грн
1	2	3	4	5	6	7	8	9	10	11
1
2
3
4
5
6
7
8
9
10
Разом

У статистиці різницю  прийнято називати загальним відхиленням. Різницю  називають відхиленням, яке можна пояснити виходячи з регресійної прямої. Різницю  називають відхиленням, яке не можна пояснити, виходячи з регресійної прямої, або непояснювальним відхиленням.

Квадрати цих відхилень просумуємо за всіма індексами, та отримаємо:

,

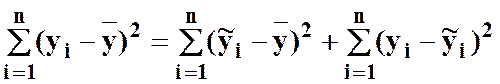де  - загальна сума квадратів, яка позначається, як правило, через SST;

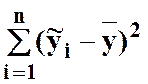 - сума квадратів, яка пояснюється регресією та позначається SSR;

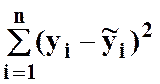 - сума квадратів помилок, яка позначається через SSE.

Отже, у скороченому вигляді можна записати SST=SSR+SSE.

Якщо поділити на n, то отримаємо вираз для дисперсій:

.

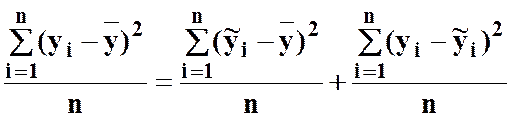Таким чином ми розклали загальну дисперсію на дві частини: дисперсію, що пояснюється регресією, та дисперсію помилок:

.

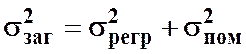Поділивши обидві частини на  отримаємо:

.

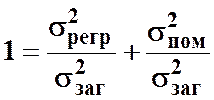Як можна побачити з цього виразу, друга частина () є частиною дисперсії, яку не можна пояснити через регресій ний зв’язок. Перша частина (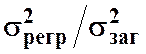) – частина дисперсії, яку можна пояснити, виходячи з регресії.

Частина дисперсії, що пояснюється регресією, називається коефіцієнтом детермінації і позначається R². Коефіцієнт детермінації використовується як критерій адекватності моделі, бо є відносною мірою варіації у під впливом незалежної змінної х. Таким чином, коефіцієнт детермінації можна записати у вигляді двох виразів, які є еквівалентними:

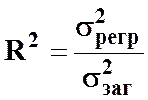 або .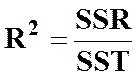

Коефіцієнт детермінації завжди додатний і знаходиться в межах від нуля до одиниці (). Коефіцієнт детермінації дорівнює квадрату коефіцієнта кореляції: .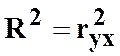

За допомогою коефіцієнта детермінації можна перевірити адекватність простої регресійної моделі. Якщо його значення близьке до одиниці, то можна вважати, що модель адекватна. Якщо його значення близьке до нуля, то модель неадекватна, тобто немає лінійного зв’язку між залежною та незалежною змінними.

Для нашого прикладу:

,

тобто дійсно існує лінійний зв’язок між вартістю основних фондів та випуском продукції.

У випадках, коли коефіцієнт кореляції має не явно виражене граничне значення (0,5;0,45;0,44 і т. ін.), важко зробити  однозначний висновок про наявність зв’язку, тобто про адекватність моделі. Отже, потрібен інший критерій, який би однозначно давав би відповідь на запитання про адекватність побудованої моделі. Найбільш поширеним з таких критеріїв є критерій Фішера.

Перевірка моделі за F-критерієм Фішера складається з певних етапів:

1 На першому етапі розраховуємо величину так званого F-відношення:

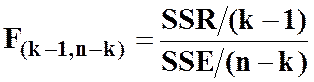 або ,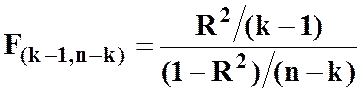

де n – кількість спостережень;

k – кількість параметрів моделі (для простої регресії k=2).

2 На другому етапі задаємо рівень значущості  або