Методичні вказівки до контрольної роботи з дисципліни "Економетрія", страница 8

3 На третьому етапі за статистичними таблицями F-розполілу Фішера зі (k-1,n-k) ступенями свободи та рівнем значущості , знаходимо критичне значення (F_кр).

4 Якщо розраховане значення , то відкидається гіпотеза Н_о, що  (або що ) з ризиком помилитись не більше ніж в  випадків.

Отже, якщо , то побудована регресійна модель адекватна реальній дійсності, тобто дійсно існує лінійний зв’язок між х та у, бо приймається гіпотеза .

Для перевірки моделі на адекватність в даному прикладі визначимо насамперед число ступенів свободи. Зв’язок між випуском продукції і вартістю основних фондів лінійний, тому рівняння простої лінійної регресії буде мати два параметри k=2 і число ступенів свободи дорівнює:  і .

Розрахункове значення F-відношення:

.

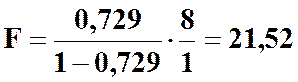За таблицею критичних значень F-розподілу Фішера (див. таблицю 11) визначаємо, що при зазначених ступенях свободи і рівні значущості  критичне значення F-критерію – F_1,8(0,05)=5,32, тобто критичне значення F-критерію менше розрахункового. Отже, побудована модель адекватна дійсності, тобто дійсно існує лінійний зв’язок між випуском продукції і вартістю основних фондів.

Таблиця 11 – Критичні значення F-критерію (рівень значущості – 0,05, тобто ймовірність Р=0,95)

К2	К1
	1	2	3	4	5	6	7	8	9
4	7,71	6,94	6,59	6,39	6,26	6,16	6,09	6,04	6,00
5	6,61	5,79	5,41	5,19	5,05	4,95	4,88	4,82	4,77
6	5,99	5,14	4,76	4,53	4,39	4,28	4,21	4,15	4,10
7	5,59	4,74	4,35	4,12	3,97	3,87	3,79	3,73	3,68
8	5,32	4,46	4,07	3,84	3,69	3,58	3,50	3,44	3,39
9	5,12	4,26	3,86	3,63	3,48	3,37	3,25	3,23	3,18
10	4,96	4,10	3,71	3,48	3,33	3,22	3,14	3,07	3,02

Методичні вказівки до завдання 3

Завдання виконується за темою ”Узагальнена модель простої лінійної регресії”.

Вибіркові лінійні регресійні моделі правильні тільки для однієї вибірки. Якщо розглянути всю генеральну сукупність, з якої обирається вибірка, то правильною для неї буде модель:

,

де  - дійсні параметри всієї генеральної сукупності;

 - неспостережувана випадкова величина.

Цю модель називають узагальненою регресивною моделлю.

Якщо параметри вибіркової лінійної моделі розраховані за методом найменших квадратів, то при виконанні класичних припущень загальної лінійної моделі математичні сподівання параметрів  дорівнюють значенням параметрів узагальненої моделі  (яка є дійсною для всієї генеральної сукупності).

Для перевірки статистичної значущості параметрів вибіркової простої регресії а₀ і а₁ використовується t-тест Ст’юдента, розрахункове значення t-критерія можна отримати за формулою:

,

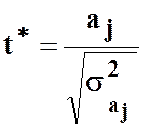де   ;   ;   ;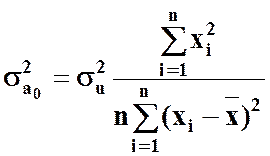

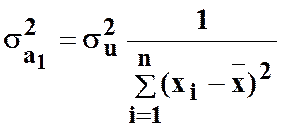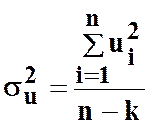 - оцінка дисперсії залишків;

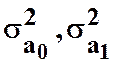 - дисперсії оцінок параметрів моделі;

k – кількість оцінених параметрів (для простої регресії k = 2, бо оцінюються параметри а₀ і а₁).

t^* порівнюється з табличним значенням, яке дає змогу знайти критичну область з (n-k) ступенями свободи. Для знаходження критичного значення потрібно задати рівень значущості . Потім за таблицями t‑розподілу Ст’юдента (див. таблицю 12) при заданому рівні значущості та ступенях свободи (n-k) знайти відповідне критичне значення (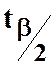). Якщо значення t^* потрапляє не в критичну зону, тобто 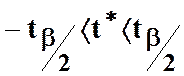, то можна зробити висновок, що з ймовірністю () оцінка а_j є статистично незначущою (тобто, приймається гіпотеза, що ). У протилежному випадку оцінка а_jє статистично значимою.

Для того, щоб визначити, як параметри a₀ і a₁ пов’язані з параметрами  і , потрібно побудувати інтервали довіри для параметрів узагальненої регресійної моделі, тобто такі інтервали, в які із заданою ймовірністю потрапляють їхні значення. Для цього розраховуємо межі інтервалів: