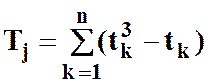Методичні вказівки до контрольної роботи з дисципліни "Економетрія", страница 5

,

де t_k - число повторень рангу k при ранжируванні чинників j-м експертом.

Для даного прикладу:

.

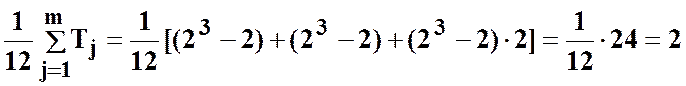Якщо збігу рангів не було, то t_k=1 та .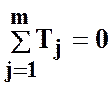

Отже  .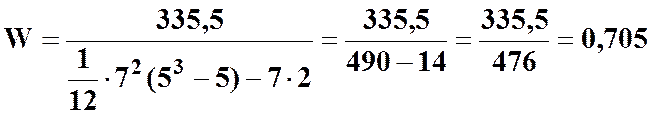

Коефіцієнт конкордації змінюється в межах

Узгодженість вважається задовільною, якщо , якщо ж , то узгодженість вважається хорошою. При повному збігу думок експертів W = 1.

Вірогідність коефіцієнта конкордації перевіряється за критерієм Пірсона, розрахункове значення якого визначається за формулою:

,

.

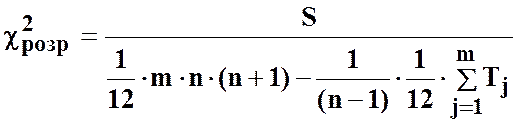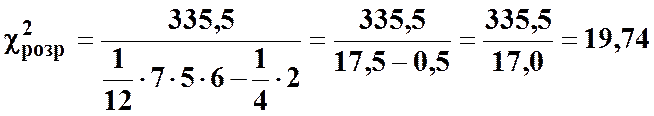Розрахункове значення 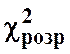 порівнюється з табличним , яке обирається з таблиці 7.

При 5% рівні значущості (тобто із ймовірністю Р = 0,95) і числі ступенів свободи , де n ‑ кількість чинників, (тобто ), табличне значення критерію Пірсона .

Якщо розрахункове значення 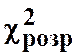 перевищує табличне, то гіпотеза про наявність згоди думок 7 експертів при ранжируванні 5 чинників приймається, тобто можна стверджувати, що має місце невипадкова узгодженість думок експертів, тому за думкою обраних експертів можна здійснювати вилучення чинників, що найбільш впливають на показник ”плинність робочих кадрів на підприємстві”.

Таблиця 7 - Критичні значення критерію  Пірсона

Р
0,90	0,95	0,975	0,99
2,71	3,84	5,02	6,63	1
4,61	5,99	7,38	9,21	2
6,25	7,81	9,35	11,34	3
7,78	9,49	11,14	13,28	4
9,24	11,07	12,83	15,09	5
10,65	12,59	14,45	16,81	6
12,02	14,07	16,01	18,48	7
13,36	15,51	17,53	20,09	8
14,68	16,92	19,02	21,67	9
15,99	18,31	20,48	23,21	10

Для вилучення найбільш впливових чинників будується діаграма убування впливу чинників (рисунок 1). Ця діаграма будується по стовпцю таблиці 6 ”Підсумкова вага”.

Рисунок 1 – Діаграма убування впливу чинників

Аналіз діаграми показує, що показник ”плинність робочих кадрів на підприємстві" у найбільшому ступені залежить від двох чинників:

Х₂ – низький рівень заробітної плати на підприємстві;

Х₁ – незадовільна забезпеченість житлом.

Тому для подальшого аналізу відбираються чинники Х₂ і Х₁.

Методичні вказівки до завдання 2

Завдання виконується за темою ”Проста вибіркова регресія”.

Прості парні лінійні регресійні моделі встановлюють лінійну залежність між двома змінними. При цьому одна із змінних вважається залежною (у) та розглядається як функція незалежної змінної (х).

У загальному вигляді проста вибіркова регресійна модель записується таким чином:

,

де у - вектор спостережень за залежною змінною: ;

х - вектор спостережень за незалежною змінною: ;

 - невідомі параметри регресійної моделі;

 - вектор випадкових величин (помилок): .

Регресійна модель називається лінійною, якщо вона лінійна за своїми параметрами. Її можна трактувати як пряму на площині, де а₀ - перетин з віссю ординат, а а₁ - нахил ( звичайно, якщо абстрагуватись від випадкової величини u).

Щоб мати явний вигляд залежності  необхідно знайти (оцінити) невідомі параметри  цієї моделі. Для цього розглянемо  пряму . Відхилення (помилки) теоретичних значень від фактичних можна виразити формулою:

, ,

де  - і-та точка на прямій, яка відповідає значенню х_і.

Відхилення, або помилки, іноді називають залишками. Логічно, що пряму треба проводити таким чином, щоб сума квадратів помилок була мінімальною. У цьому й полягає критерій найменших квадратів. Невідомі параметри  знаходяться таким чином, щоб мінімізувати 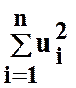, тобто маємо цільову функцію:

.

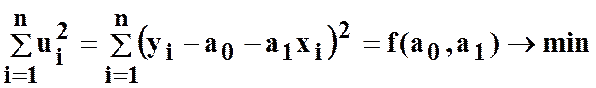Мінімізація цієї функції, яка є функцією від двох невідомих , дає таку формулу для параметра a₁ (нахилу прямої):

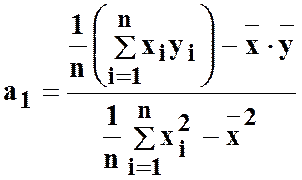, де ; .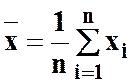

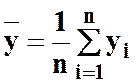Цей вираз можна переписати таким чином:

.

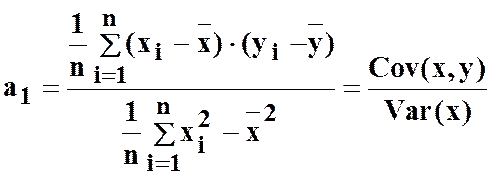При цьому параметр a₀ (перетин) знаходиться за формулою:

.

Приклад виконання завдання 2