Методичні вказівки до контрольної роботи з дисципліни "Економетрія", страница 6

Застосування простої регресійної моделі дає можливість записати зв’язок між ознаками аналітично (у вигляді рівняння) і надати йому кількісний вираз.

Розглянемо побудову простої лінійної регресійної моделі на конкретному прикладі залежності обсягу випуску продукції від вартості основних фондів підприємства (див. таблицю 8).

Таблиця 8 - Вартість основних фондів і випуск продукції по групі заводів

Номер спостереження	1	2	3	4	5	6	7	8	9	10

Аналіз даних показує, що зі збільшенням вартості основних фондів зростає і випуск продукції. Щоб виявити, на скільки підвищується в середньому випуск продукції при збільшенні основних фондів на 1 млн. грн, побудуємо модель , якщо припустити існування прямолінійного зв’язку між вартістю основних фондів і випуском продукції, який виражається рівнянням прямої .

Для оцінки параметрів прямої побудуємо розрахункову таблицю (див. таблицю 9).

Таблиця 9

Номер спостереження
1		3	4	5	6
1
2
3
4
5
6
7
1
8
9
10
Разом

За даними розрахункової таблиці отримаємо:

; ; ; ;

;

.

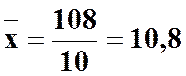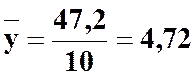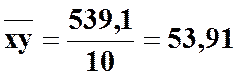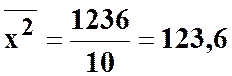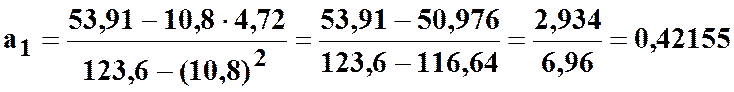Рівняння прямої буде мати такий вигляд:

.

Параметр a₁ показує, що із збільшенням вартості основних засобів на 1 млн. грн, випуск продукції збільшується в середньому на 0,42155 млн. грн. Параметр a₀ – вільний член рівняння. Він характеризує значення  при х = 0, в нашому випадку  при х = 0.

Підставимо значення незалежної змінної х в рівняння прямої  і знайдемо теоретичні, вирівняні значення у:

;

і так далі.

Теоретичні значення  надані в таблиці 9.

Критерієм, що характеризує щільність зв’язку між залежною змінною у і незалежною х, тобто наскільки значним є вплив змінної х на у, є коефіцієнт кореляції:

.

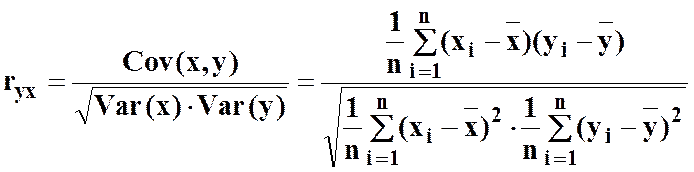  Коефіцієнт кореляції є відносною мірою зв’язку між двома змінними. Тому значення коефіцієнта кореляції завжди знаходиться в межах –1 та +1 (). Додатне значення коефіцієнта кореляції свідчить про прямий, а від’ємне – про зворотній зв’язок між змінними. Коли коефіцієнт кореляції прямує за абсолютною величиною до 1 (), то це свідчить про наявність міцного зв’язку, тобто щільність зв’язку велика. В протилежному випадку, коли коефіцієнт кореляції прямує до 0 () – зв’язок відсутній.

Для розрахунку коефіцієнта кореляції використовуємо розрахункову таблицю 10. Два останні стовпці таблиці 10 використовуються при виконанні завдання 3.

За даними таблиці 10 знаходимо:

; ;

.

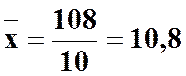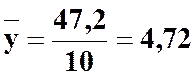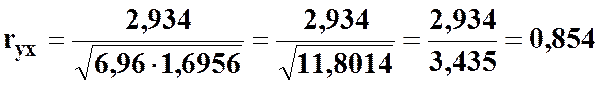Коефіцієнт кореляції пов’язаний з нахилом регресійної лінії, тобто параметром a₁ та середніми квадратичними відхиленнями  і  таким співвідношенням:

.

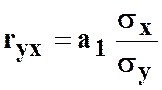Відхилення фактичних значень у від середнього значення  можна записати у вигляді:

.

Таблиця 10 – Розрахунок щільності зв’язку між вартістю основних фондів і випуском продукції по групі заводів