Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Саратовский государственный технический университет
Балаковский институт техники, технологии и управления
ПОСТРОЕНИЕ ОДНОМЕРНЫХ МОДЕЛЕЙ МЕТОДОМ
НАИМЕНЬШИХ КВАДРАТОВ
Методические указания
к выполнению лабораторных работ
по курсу “Идентификация и диагностика систем”
для студентов специальности 210100
дневной, вечерней и заочной форм обучения
Одобрено
редакционно-издательским советом
Балаковского института техники,
технологии и управления
Балаково 2009
Лабораторная работа № 1
Построение линейной одномерной модели методом
наименьших квадратов
Цель работы - освоение алгоритма метода наименьших квадратов. Освоение основных приемов работы в электронных таблицах EXCEL.
ОСНОВНЫЕ ПОНЯТИЯ
При проведении исследований часто приходится отыскивать и изучать связи между различными процессами и их характеристиками.
Если некоторая величина ![]() однозначно связана с некоторой величиной
однозначно связана с некоторой величиной
![]() , то такая связь называется функциональной
, то такая связь называется функциональной
![]() .
.
На практике между двумя случайными величинами может существовать стохастическая связь, проявляющаяся в изменении закона распределения этих величин, обнаруживать эту связь удается, как правило, только в результате многочисленных измерений и последующей статической обработки полученных результатов.
Для установления вида зависимости, при стохастической связи величины, т.е. для идентификации этой зависимости используется регрессионный анализ.
При этом различают положительную линейную и нелинейную, отрицательную и неотрицательную регрессии.
Функция регрессии определяется в виде соответствующего математического уравнения того или иного типа.
С помощью функции регрессии можно установить значение зависимой величины внутри интервала, заданные значения независимой переменной или же оценить в течение процесса внезапного интервала.
Под этой зависимостью понимают одностороннюю стохастическую связь.
![]()
![]() (1)
(1)
Неизвестные параметры регрессии ![]() и
и ![]() вычисляются
с помощью наименьших квадратов по уравнению:
вычисляются
с помощью наименьших квадратов по уравнению:
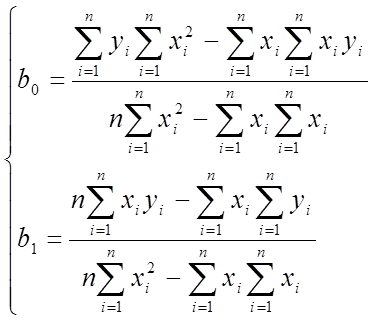 (2)
(2)
Помимо простой линейной регрессии может использоваться множественно линейная регрессия вида:
![]() (3)
(3)
В этом случае, переменные ![]() оказывают соответственное влияние на
зависимую переменную
оказывают соответственное влияние на
зависимую переменную ![]() .
.
Задачами регрессионного анализа являются: установление формы зависимости между переменными, оценка функций регрессии, оценка неизвестных значений зависимой переменной (прогноз).
Односторонняя зависимость случайной зависимой переменной Y от одной или нескольких независимых переменных X называется объясняющей регрессией. Такая зависимость может возникать тогда, когда при каждом фиксированном значении X, соответствующее значение Y подвержено случайному разбросу неконтролируемых факторов. Такая зависимость Y(X) называется регрессионной. Она может быть представлена в виде модельного уравнения регрессии:
![]() , (4)
, (4)
где ![]() - случайная переменная,
характеризующая отклонение от функции регрессии.
- случайная переменная,
характеризующая отклонение от функции регрессии.
Линейный регрессионный анализ - это анализ, для которого функция f(X) линейна относительно оцениваемых факторов.
Регрессионный анализ включает в себя две основные компоненты:
1) оценка вектора коэффициентов с помощью метода наименьших квадратов;
2) дисперсионный анализ – для оценки адекватности модели.
Для того чтобы провести регрессионный анализ необходимо:
ü чтобы количество экспериментальных данных было больше либо равно 30 на один вход;
ü распределение выходной величины должно быть нормальным;
ü в процессе эксперимента дисперсия
выходной величины Yне меняется: ![]() ;
;
ü переменная X изменяется с пренебрежительно малыми ошибками, то есть является детерминированной;
ü выходные переменные X1, X2, … Xn стахостически независимы между
собой: ![]() ;
;
ü дискретность проведения экспериментов
во времени ![]() берется таким образом, чтобы
последовательно взятые значения Y1, Y2, Y3 были стахостически независимыми, то
есть
берется таким образом, чтобы
последовательно взятые значения Y1, Y2, Y3 были стахостически независимыми, то
есть ![]() больше времени затухания автокорреляционной
функции;
больше времени затухания автокорреляционной
функции;
ü учет динамики в регрессионном анализе производится в виде транспортного запаздывания, которое определяется как время нахождения максимума взаимно корреляционной функции X и Y.
На основании этих предпосылок получают уравнение регрессионной модели методом наименьших квадратов.
Алгоритм расчета уравнения линейной регрессии МНК
1.
Проводим
эксперимент, задаем не менее 30 значений X, ![]() ,
, ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.