5. Вид модального уравнения регрессии.
6. Что такое линейный регрессионный анализ?
7. Компоненты регрессионного анализа.
8. Как рассчитываются коэффициенты одномерной линейной регрессионной модели.
9. Как рассчитать 95% ошибку аппроксимации.
ВРЕМЯ, ОТВЕДЕННОЕ НА ВЫПОЛНЕНИЕ РАБОТЫ
Подготовка к работе – 0,5 акад. часа.
Выполнение работы – 0,5 акад. часа.
Расчеты на ЭВМ – 0,5 акад. часа.
Оформление работы – 0,5 акад. часа.
ЛитЕратура
1. Идентификация объектов управления: учеб. пособие. / А. Д. Семенов, Д. В. Артамонов, А. В. Брюхачев. - Пенза: ПГУ, 2005. - 211 с.
2. Основы теории идентификации объектов управления: учеб. пособие. / А.А. Игнатьев, С.А. Игнатьев. - Саратов: СГТУ, 2008. - 44 с.
3. Теория вероятности и математическая статистика в примерах и задачах с применением EXCEL. / Г.В. Горелова, И.А. Кацко. - Ростов н/Д: Феникс, 2006.- 475 с.
Лабораторная работа № 2
Построение нелинейной одномерной модели методом
наименьших квадратов
Цель работы - освоение метода построения нелинейной модели с применением линеаризации; освоение метода оценки адекватности модели и ошибки аппроксимации; автоматизация процесса построения математической модели; освоение основных приемов работы в электронных таблицах EXCEL.
ОСНОВНЫЕ ПОНЯТИЯ
Под нелинейной регрессией понимают более сложную одностороннюю стохастическую зависимость. Наиболее часто встречаются следующие виды нелинейной регрессии:
Полиноминальное уравнение регрессии:
![]()
![]() , (7)
, (7)
Гиперболическое уравнение регрессии:
![]() ,
(8)
,
(8)
Степенное уравнение регрессии:
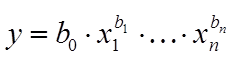 . (9)
. (9)
Могут применяться показательные, логарифмические, тригонометрические уравнения, а также полиномы Чебышева.
Обычно подбор конкретной функции осуществляется на базе той науки в рамках которой изучается данный процесс.
Принято различать два класса уравнений нелинейной регрессии.
Первый класс охватывает регрессии
нелинейные относительно входного параметра х, но линейные
относительно коэффициентов ![]() . Для таких
регрессий применим метод наименьших квадратов.
. Для таких
регрессий применим метод наименьших квадратов.
Второй класс охватывает регрессии,
которые являются нелинейными также относительно коэффициентов ![]() , что требует для применения итерационных
методов.
, что требует для применения итерационных
методов.
Достаточно часто в различных технических исследованиях используется параболическая регрессия к-го порядка.
Для случая к=2 такая регрессия имеет вид:
![]() (10)
(10)
В этом случае для нахождения коэффициентов составляется система трех уравнений:
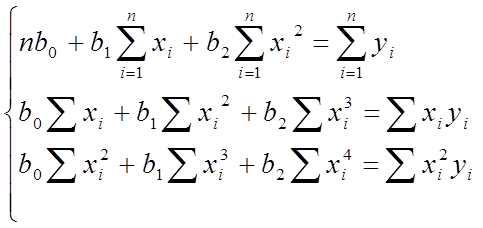 (11)
(11)
Необходимо иметь в виду, что после
вычисления коэффициента ![]() всегда должна
осуществляться проверка их значимости по соответствующей методике и незначимые
коэффициенты обнуляются.
всегда должна
осуществляться проверка их значимости по соответствующей методике и незначимые
коэффициенты обнуляются.
При использовании степенного
уравнения регрессии следует иметь в виду, что оно нелинейно относительно
параметров ![]() , однако путем логарифмирования может быть
преобразовано в линейное уравнение:
, однако путем логарифмирования может быть
преобразовано в линейное уравнение:
![]() (12)
(12)
Для определения неизвестных
параметров ![]() ,
,![]() ,…
,…![]() используется метод наименьших квадратов.
используется метод наименьших квадратов.
Построение нелинейной модели путем линеаризации
Рассмотрим пример линеаризации степенного уравнения:
![]() .
(13)
.
(13)
Проведем логарифмирование и получим:
![]() .
(14)
.
(14)
Введем обозначения:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.