Информатика и выч. техника \ Идентификация и диагностика систем управления

Построение одномерных моделей методом наименьших квадратов: Методические указания к выполнению лабораторных работ по курсу “Идентификация и диагностика систем”, страница 2

2.  Значения xi и yiи сводим их в таблицу в столбцы 2 и 3.

3.  Находим квадрат входной величины .

4.  Находим произведение входной и выходной величин .

5.  Находим сумму входной и выходной величин  .

6.  Находим квадрат суммы входной и выходной величины .

7.  Находим сумму входных величин .

8.  Находим  .

9.  Находим сумму квадратов входных величин  .

10.  Находим сумму произведений входной и выходной величин     .

11.   Находим сумму входной и выходной величин

 

12.   Находим сумму квадрата сумм и выходной величин

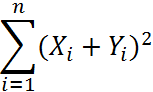
13.  (5)


 Находим коэффициентыb0 и b1по формулам:

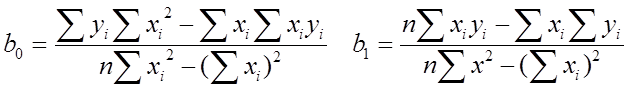По формуле линейной регрессии находим расчетные значения вы­ходных величин:    .

14.   Находим отклонение расчетного значения от фактического значе­ния выходной величины:   .

15.   Находим квадрат отклонения:  .

16.   Находим сумму квадратов отклонений:

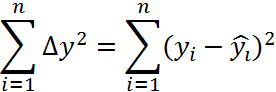
18.  Рассчитываем 95% ошибку аппроксимации:

(6)                                 ,                                      

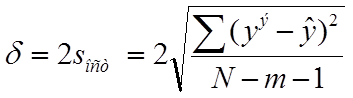где 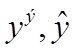- экспериментальное и расчетное значения выходной перемен­ной; N, m - соответственно, количество экспериментов и коэффициентов регрессионного уравнения (без учета b0).

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТ

1.   Подготовить в электронных таблицах EXCEL программу для реше­ния поставленной задачи:

Ввести наименование работы, фамилию студента, номер варианта работы. Подготовить таблицу, включающую:

ü номера точек по порядку;

ü значения входной переменной;

ü значения выходной переменной;

ü столбцы для промежуточных результатов вычислений;

ü ввести формулы для расчета промежуточных переменных.

Внизу таблицы в двух ячейках ввести формулы для расчета коэффи­циентов уравнения (5).          

В последних столбцах таблицы произвести расчет:

            ,     

Рассчитать 95% ошибку аппроксимации

                           ,

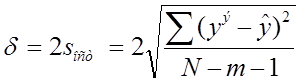где - экспериментальное и расчетное значения выходной перемен­ной; N, m - соответственно, количество экспериментов и коэффициентов регрессионного уравнения (без учета b0).

2.  Построить графики зависимости экспериментальных и рассчитан­ных значений выходной переменной  от входной переменной.

3.  Провести анализ адекватности полученного уравнения.

4.  Построить линию тренда и показать уравнение и R2 на диаграмме.

5.  Отформатировать все элементы таблицы и графики.

6.  Скопировать исходные данные на второй лист вашей книги.

7.   На 2 листе не пользуясь формулами для нахождения коэффициен­тов b0 и b1, подобрать их по критерий  .  Используйте команду Поиск решения.

8.  Распечатать работу.

ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ

Задан линейный статический объект с 1 входом и 1 выходом.

Имеется выборка пассивного эксперимента объемом 21 точка, со­держащая значения входной и выходной переменных.

Период выборки обеспечивает отсутствие автокорреляции Х, Y.

Необходимо найти оценки коэффициентов регрессионного уравне­ния вида   и оценку величины ошибки аппроксимации.

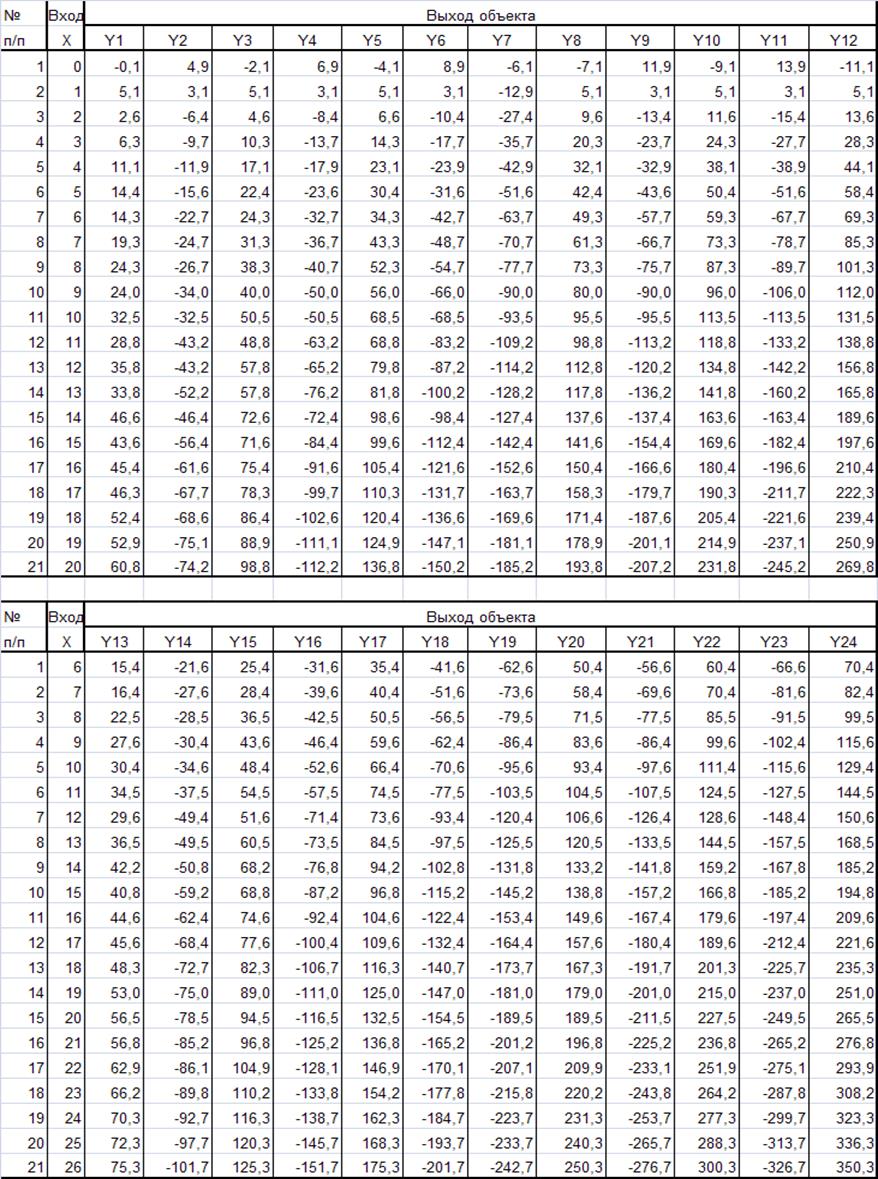
Пример лабораторной работы представлен на рисунке 1.

СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА

Отчет оформляется в текстовом редакторе Word на бумаге формата А4 ГОСТ 6656-76 (210х297 мм) и содержит:

1.  Название лабораторной работы.

2.  Цель работы.

3.  Задание.

4.  Результаты вычисления.

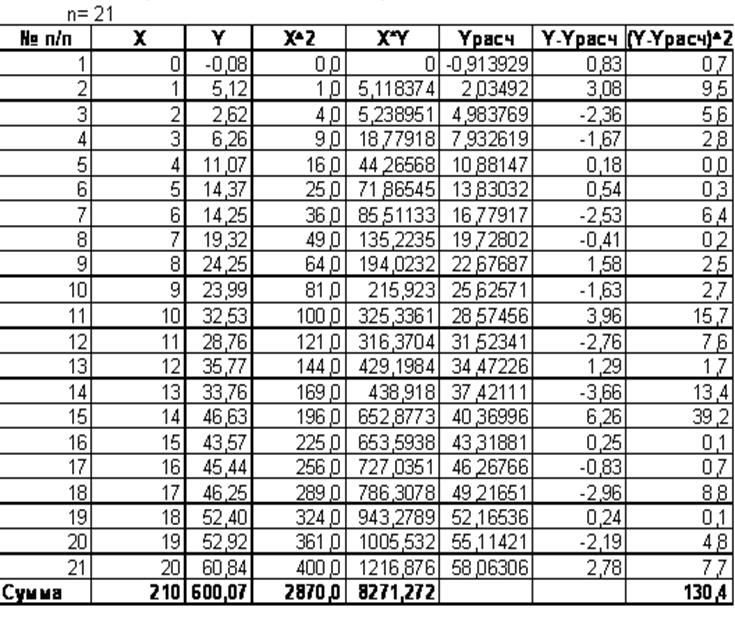
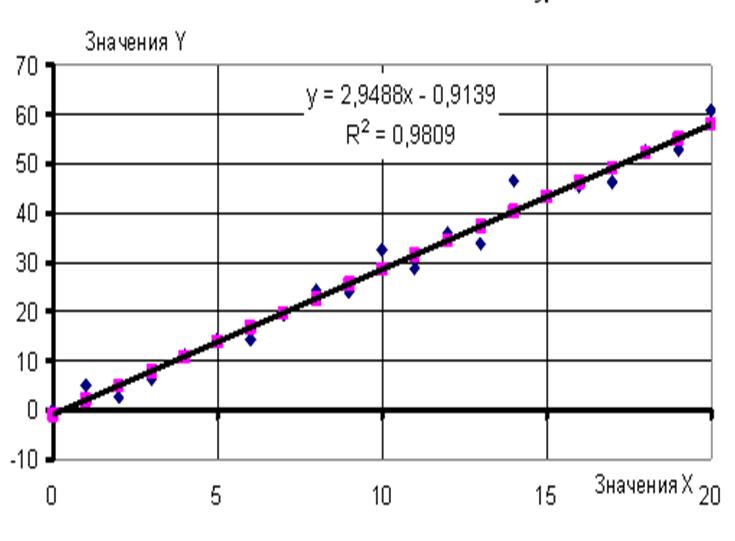
Рис. 1. Построение линейной модели методом наименьших квадратов


ВАРИАНТЫ ЗАДАНИЙ

Вариант задания выбрать по номеру в журнале.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1.  Задачи регрессионного анализа.

2.  Что называют объясняющей регрессией?

3.  Какая зависимость называется регрессионной?

4.  Предпосылки регрессионного анализа.

Скачать файл