САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ
КАФЕДРА «УПРАВЛЕНИЕ И ИНФОРМАТИКА В ТЕХНИЧЕСКИХ СИСТЕМАХ»
ПРАКТИЧЕСКАЯ РАБОТА №4
по дисциплине «ИДС»
ПРОХОЖДЕНИЕ СЛУЧАЙНОГО СИГНАЛА
ЧЕРЕЗ ИНЕРЦИОННОЕ ЗВЕНО I ПОРЯДКА
Вариант №7
Выполнил: ст.гр. УИТ-41
Душина Д.В.
Принял:
Стельмах И.В.
2011
1. Задаём характеристики случайного процесса (среднее x1, СКО, s1) и параметры звена первого порядка (k, T).
x1=10*N=60, где N=6;
s1=M=4;
k=N=6;
T=M=4.
где N, М-количество букв в фамилии, имени студента.
Выбираем количество точек 512. m=9, n=2m=29=512
2. Генерируем нормальный случ.процесс с заданными характеристиками:
i=0..n-1 x=rnorm(n,x1,s1)
|
|
3. Находим оценки характеристик случ.процесса:
x0=58.244 x511=62.337
mean(x)=59.582 var(x)=15.996 stdev(x)=4
4. Вводим обозначения:
xsr=mean(x) xsr=59.582 sx=stdev(x) sx=4
5. Пропустим сгенерированный случ.процесс через звено первого порядка. Используем разностное уравнение звена первого порядка.
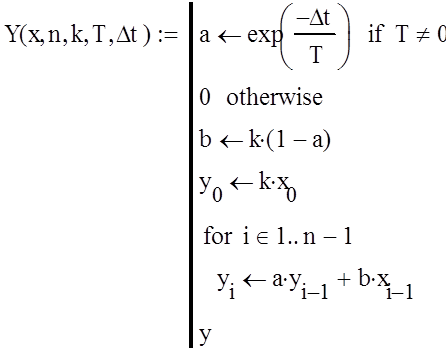
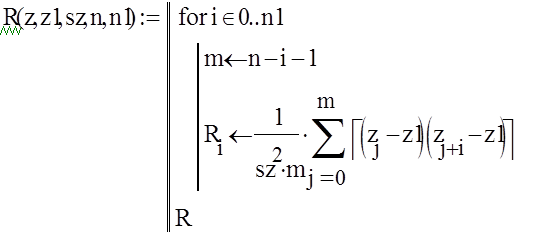
Принимаем дискретность по времени ∆t=0.1
6. Строим графики входного и выходного сигналов. y=Y(x,n,k,T,∆t)
|
|
y1=mean(y) y1=356.709 sy=stdev(y) sy=3.097
7. Расчёт автокорреляционной функции входного и выходного временных рядов. Количество ординат корреляционной функции принимаем n1=127
j=0..n1 Rxx=R(x,xsr,sx,n,n1) Rxx0=1.002 Ryy=R(y,mean(y),stdev(y),n,n1)
8. Строим графики автокорреляционных функций
|
|
9. Исследуем влияние постоянной времени фильтра на выходной временной ряд и его корреляционную функцию. Для этого расчитываем временные ряды и автокорреляционные функции для постоянных времени фильтра 0, 5, 10, 40 и строим их графики.
z1=Y(x,n,k,0,∆t) Rz1=R(z1,mean(z1),stdev(z1),n,n1)
z2=Y(x,n,k,5,∆t) Rz2=R(z2,mean(z2),stdev(z2),n,n1)
z3=Y(x,n,k,10,∆t) Rz3=R(z3,mean(z3),stdev(z3),n,n1)
z4=Y(x,n,k,40,∆t) Rz4=R(z4,mean(z4),stdev(z4),n,n1)
|
|
|
|
10. По автокорреляционным функциям временных рядов получим спектральные плотности входного х и выходного z сигналов.
j=0..127 Rxx0=1.002 Rxx127=-0.044 Rxx128=
Sx=fft(Rxx) Sz1=fft(Rz1) Sz2=fft(Rz2) Sz3=fft(Rz3) Sz4=fft(Rz4)
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.