Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Саратовский государственный технический университет
Балаковский институт техники, технологии и управления
РЕГРЕССИОННОЙ АНАЛИЗ В ПАКЕТЕ EXCEL
Методическое указание к выполнению лабораторной работы
по дисциплине “Идентификация и диагностика систем управления”
для студентов специальности 220201
очной и заочной форм обучения
Одобрено
редакционно-издательским советом
Балаковского института техники,
технологии и управления
Балаково 2010
Цель работы: Освоение регрессионного анализа в пакете EXCEL.
ОСНОВНЫЕ ПОНЯТИЯ
Задачами регрессионного анализа являются: установление формы зависимости между переменными, оценка функций регрессии, оценка неизвестных значений зависимой переменной (прогноз).
Односторонняя зависимость случайной зависимой переменной Y от одной или нескольких независимых переменных Х называется объясняющей регрессией.Такая зависимость может возникать тогда, когда при каждом фиксированном значении X, соответствующее значение Y подвержено случайному разбросу под воздействием неконтролируемых факторов. Такая зависимость Y(X) называется регрессионной. Она может быть представлена в виде модельного уравнения регрессии:
![]() (1)
(1)
где ![]() - случайная переменная характеризующая отклонение
функции регрессии.
- случайная переменная характеризующая отклонение
функции регрессии.
Линейный регрессионный анализ - это анализ, для которого функция f(X) линейна относительно оцениваемых факторов. Уравнение линейной регрессии имеет вид:
![]() (2)
(2)
Регрессионный анализ включает в себя две основные компоненты:
1) оценка вектора
коэффициентов с помощью метода наименьших квадратов: ![]() ;
;
2) дисперсионный анализ.
Для проведения регрессионного анализа необходимо:
1) чтобы количество экспериментальных данных было больше либо равно 30 на один вход;
2) распределение выходной величины должно быть нормальным;
3) в процессе эксперимента дисперсия
выходной величины Y
не меняется: ![]() ;
;
4) переменная X является детерменированой;
5) выходные переменные Y1, Y2, … Yn стохастически независимы между
собой: ![]() ;
;
6) дискретность проведения экспериментов
во времени ![]() берется таким образом, чтобы
последовательно взятые значения Y1, Y2, … Yn были стохастически независимы, то
есть
берется таким образом, чтобы
последовательно взятые значения Y1, Y2, … Yn были стохастически независимы, то
есть ![]() больше времени затухания
автокорреляционной функции;
больше времени затухания
автокорреляционной функции;
7) учет динамики в регрессионном анализе производится в виде транспортного запаздывания, которое определяется как время нахождения максимума взаимно корреляционной функции X и Y.
На основании этих предпосылок получают уравнение регрессионной модели методом наименьших квадратов.
Задача дисперсионного анализа заключается в определении той части экспериментальных данных, которая описывается регрессионной моделью (определяется коэффициент детерминации R2 ), а также определение адекватности регрессионной модели. Для этого используется основное уравнение дисперсионного анализа, которое имеет вид:
![]() (3)
(3)
где 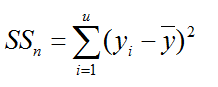 - полная сумма квадратичных отклонений
характеризует разброс значений выходной величины y вокруг его среднего значения
- полная сумма квадратичных отклонений
характеризует разброс значений выходной величины y вокруг его среднего значения ![]() ;
; 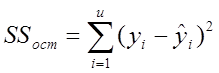 - остаточная сумма отклонений
используется в качестве критерия МНК;
- остаточная сумма отклонений
используется в качестве критерия МНК; 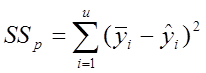 - сумма квадратичных отклонений расчетных значений
выходной величины
- сумма квадратичных отклонений расчетных значений
выходной величины ![]() от среднего значения
от среднего значения ![]() .
.
Коэффициент детерминации R2 определяется соотношением суммы обусловленной регрессией и остаточной суммы отклонений:
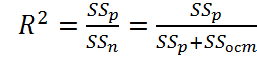 (4)
(4)
Коэффициент детерминации изменяется от 0 до 1:
![]()
При ![]() коэффициент детерминации
коэффициент детерминации ![]() а при
а при ![]() коэффициент детерминации
коэффициент детерминации ![]() . Чем ближе коэффициент детерминации
к 1, тем точнее регрессионная модель.
. Чем ближе коэффициент детерминации
к 1, тем точнее регрессионная модель.
При малых объемах выборки (N<30) используется коэффициент множественной корреляции:
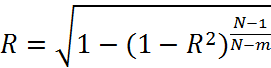 ,
(5)
,
(5)
где N – количество выборки; m – количество входов.
Для оценки адекватности регрессионной модели используется критерий Фишера, который определяется отношением дисперсии обусловленной регрессией и остаточной дисперсией:
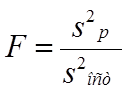 , (6)
, (6)
Дисперсия, обусловленная регрессией - среднее значение квадратов отклонения обусловленных регрессией, определяется выражением:
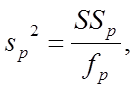 (7)
(7)
где fр- число степеней свободы суммы обусловленной регрессией:
![]() ,
(8)
,
(8)
где m – количество входов.
Остаточная дисперсия определяется выражением:
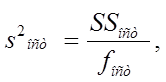 (9)
(9)
где fост- число степеней свободы остаточной суммы:
![]() ,
(10)
,
(10)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.