Построение моделей объектов управления по переходным характеристикам: Методическое указание к выполнению лабораторной работы

Министерство образования и науки Российской Федерации

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

КОНТРОЛЬНАЯ РАБОТА №2

Методическое указание к выполнению контрольной работы

по дисциплине “Идентификация и диагностика систем управления”

для студентов специальности 220201.65

заочной формы обучения

Одобрено

редакционно-издательским советом

Балаковского института техники,

технологии и управления

Методическое указание рекомендовано  на заседании кафедры

“Управление и информатика в технических системах”

“ 30 ” августа  2011 г.

Протокол №  1

       Зав. кафедрой _______________ Т.Н. Скоробогатова

Балаково 2011

Цель работы: Освоить метод нелинейного программирования и по­лу­чить навыки построения динамических моделей по переходным характе­ристикам в Excel.

ОСНОВНЫЕ ПОНЯТИЯ

В данной работе строятся математические моделиобъектов первого, второго порядка и реального интегрирующего звена.

1.  Дифференциальное уравнение объекта управления апериодического звена первого порядка:    

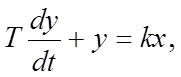                                                                             (1)

где x– входная величина; y- выходная величина.

Структурная схема объекта управления апериодического звена первого порядка представлена на рисунке 1.

 

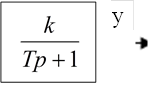Рис. 1 - Структурная схема объекта управления апериодического

звена первого порядка

Разностное уравнение при периоде дискретизации  объекта  пер­вого порядка:    

                                                                                (2)

где a, b – коэффициенты, вычисляемые по формулам:

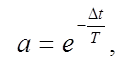
                                                                     (3)

где k- коэффициент усиления звена; Т - постоянная времени звена.

2.  Дифференциальное уравнение объекта управления апериодического звена второго порядка:

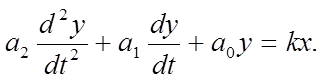                                                                    (4)

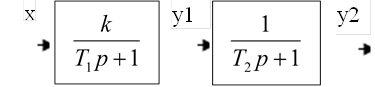
Структурная схема объекта управления апериодического звена второго порядка может быть представ­лена в виде последовательного соединения двух элементов первого по­рядка рисунок 2.

 

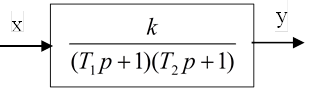Рис. 2 - Структурная схема объекта управления апериодического

звена второго порядка

Разностные уравнения, описывающие два последовательно соединенных звена первого порядка, имеют вид:  

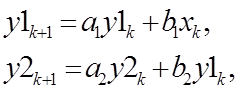                                                                               (5)

Коэффициенты уравнений находятся по формулам:

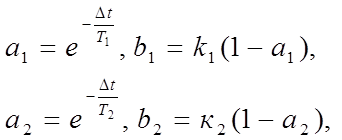                                                                            (6) 

где k₁ ,k₂ - коэффициенты усиления звеньев; Т₁,Т₂ - постоянные времени звеньев.

3.  Дифференциальное уравнение объекта управления реального интегрирующего звена имеет вид:

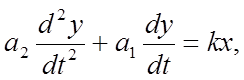                                                                          (7)     

Структурная схема объекта управления реального интегрирующего звена может быть представлена в виде по­следовательного соединения двух звеньев:

 

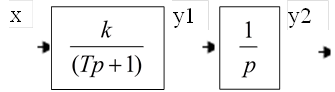Рис. 3 - Структурная схема реального интегрирующего объ­екта управления

Разностные уравнения, описывающие два последовательно соединенных звена, имеют вид:

                                                                                 (8)

где a, b – коэффициенты, вычисляемые по формулам:

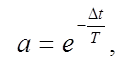
                                                                         (9)

где k- коэффициент усиления апериодического звена; Т - постоянная времени апериодического звена.

Задача нелинейного программирования  - подобрать такой вектор параметров модели B, чтобы при выбранном  уравнении модели объекта   критерий оптимизации I, рав­ный сумме квадратов отклонений между расчетными и эксперимен­таль­ными  значениями, был минимальным:

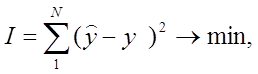                                                                      (10)

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Даныэкспериментальные данные переходных характеристик раз­личных объектов при ступенчатых изменениях входного сигнала. Необ­хо­димо выбрать вид уравнений моделей и методом нелинейного про­грамми­рования  найти оценки их параметров.

Взять у преподавателя номер варианта и экспериментальные данные по трем переходным процессам в таблицах 1,2,3.

1.  Создать таблицу и ввести исходные данные – количество точек N, зна­чения  для трех экспериментов.

2.  Построить график зависимости для первого эксперимента.

3.  По виду графика выбрать вид модели. 

4.  Выделить ячейки для параметров выбранной модели и вве­сти на­чальные значения k - коэффициента усиления и T- постоянной времени звена, определенные по графику.

5.  Рассчитать коэффициенты a,b разностного уравнения по выражениям (3,6,9).  

6.  Рассчитать выходную переменную по раз­ностным уравнениям (2,5,8).

7.  Рассчитать 95% ошибку аппроксимации по выражению: 

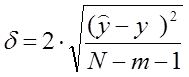                                ,                                                    (11)

где N - количество экспериментов , m – число входных величин.

8.  На диаграмме выходной переменной построить график , рас­считанный при начальных значениях коэффициентов модели.