Построение моделей объектов управления по переходным характеристикам: Методическое указание к выполнению лабораторной работы, страница 2

9.  Используя алгоритм нелинейного программирования  Excel «По­иск решения»: найти параметры модели, дающие минимальное значе­ние критерия.

Войти в «Поиск решения»  (Данные/Пакет данных/Поиск ре­ше­ния) и ввести исходные данные в диалоговом окне:

ü  «Установить целевую ячейку»  - указать адрес ячейки критерия пер­вой модели .

ü  Включить флажок поиска минимума   -  «минимальное значе­ние».

ü  В строке «изменяя ячейки» - указать ячейки искомых коэффи­циен­тов К, Т.

ü  Войти в «Параметры»  и включить «Автомасштабирование»

ü  Запустить программу путем нажатия кнопки «Выполнить»

Программа «Поиск решения» начнет подбирать коэффициенты мо­дели, добиваясь получения минимального значения критерия. После окончания работы программы в ячейках коэффициентов бу­дут най­денные значения.

10.  На диаграмме проконтролировать правильность решения за­дачи по наложению графика  на график .

11.   Аналогично построить модели для 2-го и 3-го объектов.

ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ

Задание1

1.  Создать таблицу и ввести исходные данные – количество точек N, зна­чения  для первого экспериментов.

2.  Построить график зависимости для первого эксперимента.

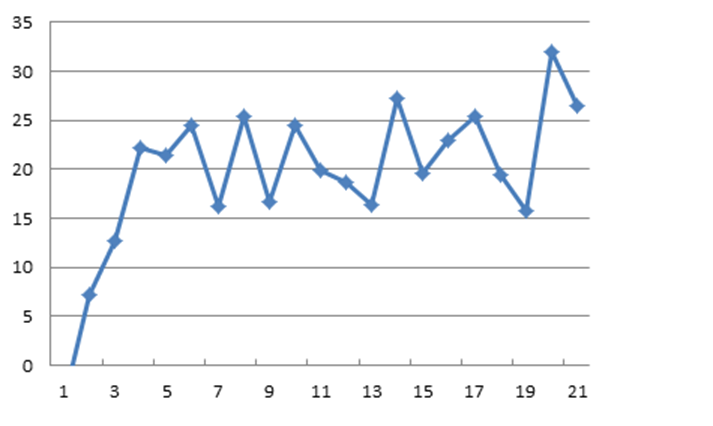
Рис.4 – График экспериментальных данных первой модели

3.  По виду графика выбрать вид модели. По графику определить коэффициент пропорциональности звена к  и его постоянную времени Т. 

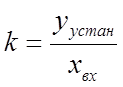                                                                                                             (12)

где y_устан- установившееся значение выходной величины; 

x_вх - значение входной величины x. 

4.   Рассчитать коэффициенты разностного уравнения по формуле (3).

5.   Рассчитать выходную переменную по раз­ностному уравнению (2).

6.   Рассчитать ошибку аппроксимации по выражению (11).                                 

7.   На диаграмме выходной переменной построить график , рас­считанный при начальных значениях коэффициентов модели рис.5.

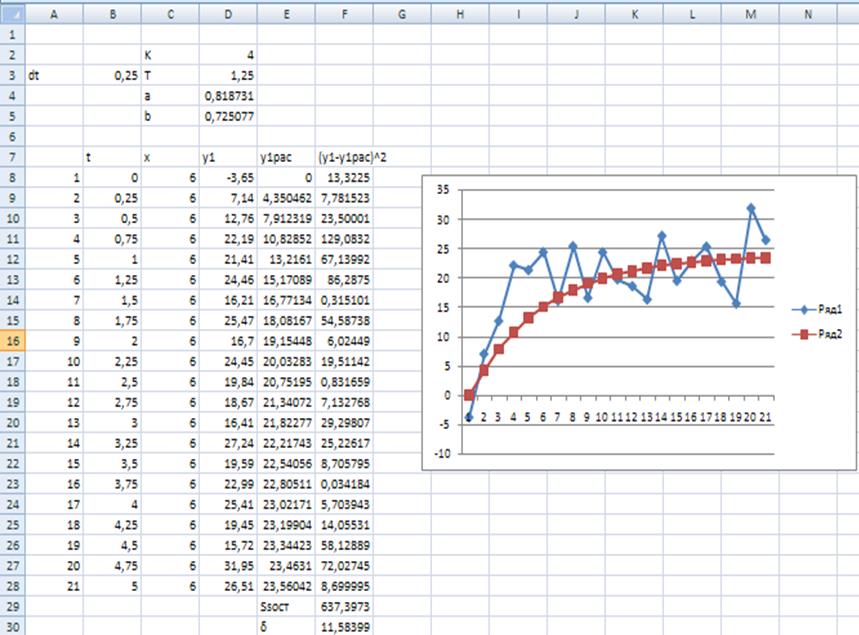
Рис. 5 -  Результаты предварительного вычисления первой модели

8.  Используя алгоритм нелинейного программирования  Excel найти параметры модели, дающие минимальное значе­ние критерия (10).  Для этого используется надстройка «Поиск решения»  (Данные/ анализ данных/Поиск ре­ше­ния). В диалоговом окне «Поиск решения» вводят исходные данные рис.6:

ü  «Установить целевую ячейку»  - указать адрес ячейки критерия пер­вой модели .

ü  Включить флажок поиска минимума   -  «минимальное значе­ние».

ü  В строке «изменяя ячейки» - указать ячейки искомых коэффи­циен­тов к, Т.

ü  Войти в «Параметры»  и включить «Автомасштабирование».

ü  Запустить программу путем нажатия кнопки «Выполнить».

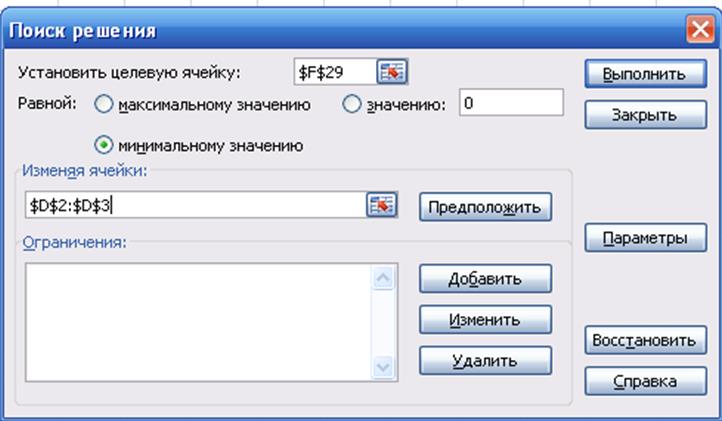
Рис.6 – Диалоговое окно надстройки «Поиск решения» 

Программа «Поиск решения» начнет подбирать коэффициенты мо­дели, добиваясь получения минимального значения критерия. После окончания работы программы в ячейках коэффициентов бу­дут най­денные значения.

9.  На диаграмме проконтролировать правильность решения за­дачи по наложению графика  на график   рис.7.

Рис.7 -   Результаты вычисления первой модели

Задание 2

1.  Создать таблицу и ввести исходные данные – количество точек N, зна­чения  для второго эксперимента.

2.   Построить график зависимости . 

3.  По виду графика рис.8 выбрать вид модели. Определить коэффициенты  первого и второго звеньев k₁ и k₂, и их постоянные времени  Т₁ и  Т₂.  Для данного примера: k₁=1; k₂=7; T₁=0,5; T₂=1.

4.  Выделить ячейки для коэффициентов выбранной модели и вве­сти на­чальные значения коэффициентов. Для расчета коэффициентов разностного уравнения использовать выражение (6).  

5.   В таблице  добавить столбец и  рассчитать промежуточную выходную переменную  y1по раз­ностному уравнению (5):

6.  В таблице  добавить столбец и  рассчитать выходную переменную y2 по раз­ностному уравнению (5).

7.  Рассчитать 95% ошибку аппроксимации по выражению (11).                                  

8.  На диаграмме выходной переменной построить график , рас­считанный при начальных значениях коэффициентов модели рис. 8.

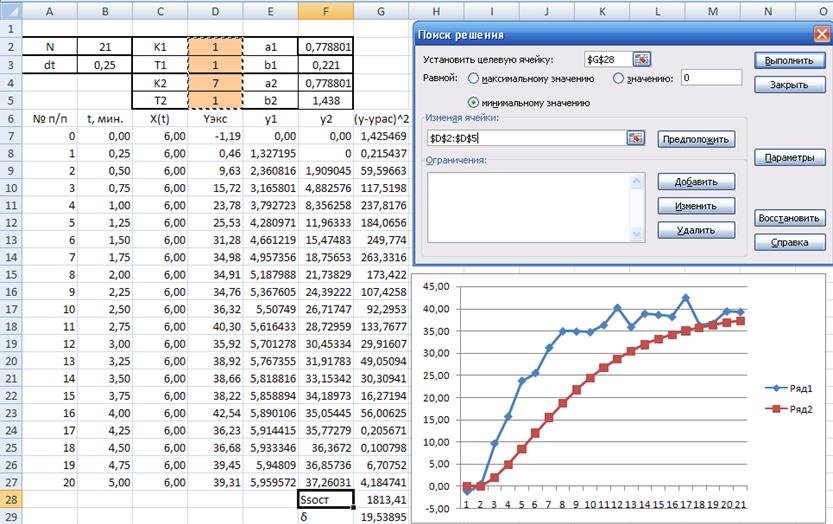
Рис. 8  Результаты предварительного вычисления второй модели