








































![]() Практическое
занятие №7.
Практическое
занятие №7.
Линейные операции над векторами.
1. Def: Направленный отрезок - вектор
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Построить:
Построить: ![]() (-1;2),
(-1;2), ![]() (3;-2;4).
(3;-2;4).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 2.
2. ![]() =
= ![]()
3. Линейные операции.
. Def: Векторы
![]() коллинеарны, если они лежат на параллельных или совпадающих
прямых.
коллинеарны, если они лежат на параллельных или совпадающих
прямых.
Признак коллинеарности: 1) ![]() êê
êê![]() .
.
2) 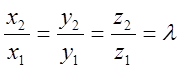
5. Def: Векторы называются компланарными, если они лежат в одной плоскости, или $ плоскости, которой все они параллельны.
6. Единичным вектором или ортом называется вектор, длина которого равна 1.
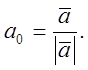
![]()
![]() 7. Def:
7. Def: ![]() называются
линейно зависимыми, если $
называются
линейно зависимыми, если $ ![]() (хотя бы
(хотя бы
одно ¹ 0 ), если имеет место нулевая комбинация: ![]()
![]()
![]()
Def: Если
равенство : ![]() выполняется
лишь при
выполняется
лишь при![]() ,то систему векторов называют линейно
независимой или базисом.
,то систему векторов называют линейно
независимой или базисом.
Пример: 1) Любая пара неколлинеарных векторов на плоскости образуют базис.
2) Любые три
неколлинеарные вектора образуют базис ир-ва и любой вектор ![]() можно представить линейной комбинацией этих векторов,
если
можно представить линейной комбинацией этих векторов,
если ![]() некомпланарны.
некомпланарны. ![]()
Запись ![]() равносильна :
равносильна : ![]() где
где ![]() - единичный базис.
- единичный базис.
Сложение. Вычитание.
![]()

![]()

![]()
![]()


![]()

Решение задач:
№ 769; 775; 776; 780; 783; (784); 787; 789(с). Самостоятельно 763; 785.
 Д.з. № 764; 778; 782; 793;
Скалярное произведение.
Д.з. № 764; 778; 782; 793;
Скалярное произведение.
Решение № 783.
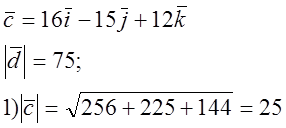
![]()
№ 784.
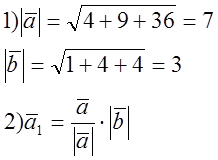
![]()
![]()

![]()
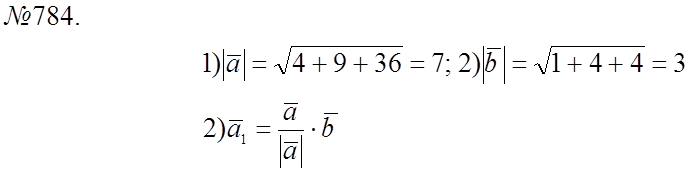
(Если ![]() является
биссектриссой, то
является
биссектриссой, то ![]() должна быть биссектриссой ромба).
должна быть биссектриссой ромба).
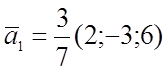
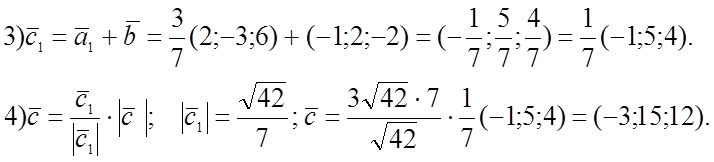
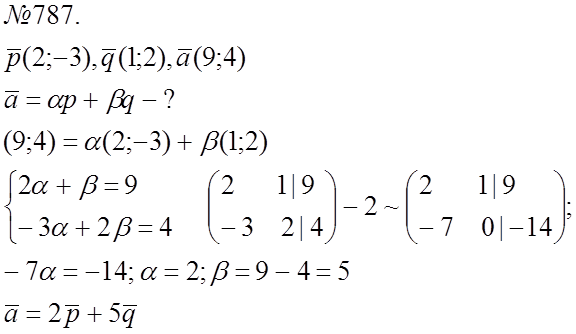
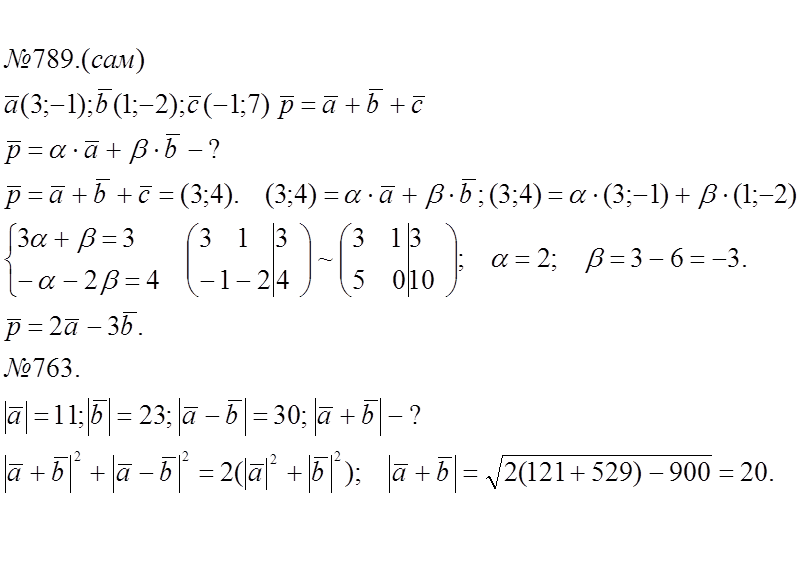
![]()



![]()

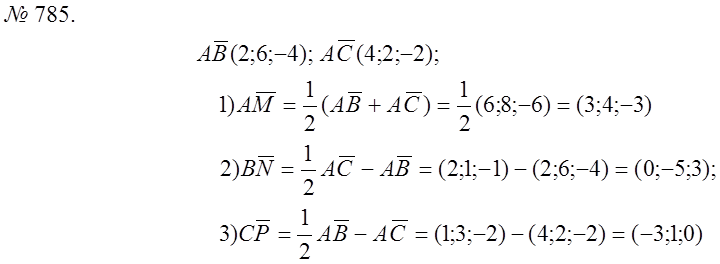 Практическое
занятие № 8. Скалярное произведение.
Практическое
занятие № 8. Скалярное произведение.
1.Def: 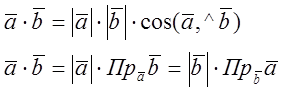
2.Запись: ![]() .
.
3.Свойства: 1)![]()
2)![]()
3)![]()
4)![]()
4. ![]()
5. 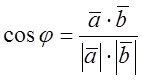 Если
Если
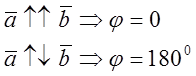
6. Механический смысл : ![]()
Решение задач.
№ 808, 815, 817, 821, 824, 833, 827, 826.
Д.з. № 822, 825, 834, 823. Учить векторное произведение.
№ 808.
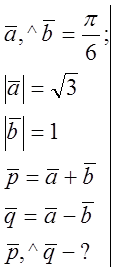
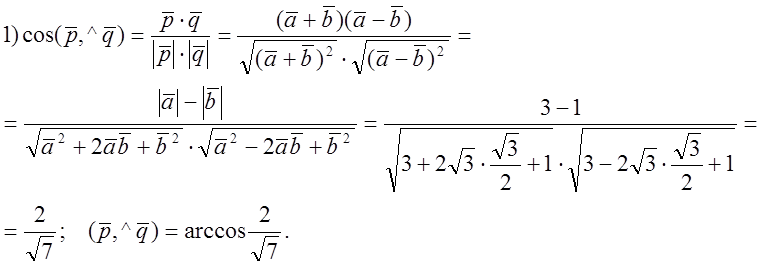
![]() № 815.
№ 815.
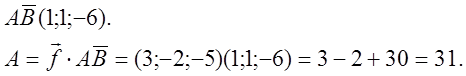
№ 817.
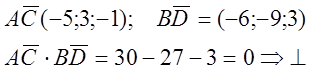
№ 821.
![]()
![]()
![]()
 B(5;1;-1)
B(5;1;-1)
C(1;-2;1)
A(3;2;-3)
1)Внешний угол :![]()
Внутренний: ![]()
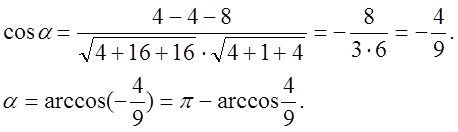
№ 824.
![]()
![]()
![]()
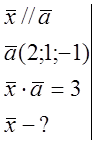
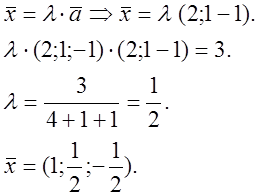
![]() № 833.
№ 833.
![]()
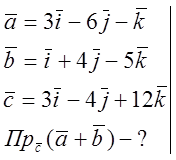
![]()
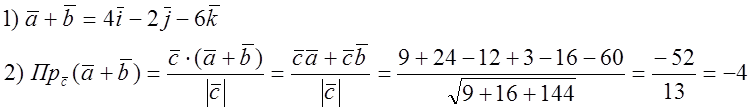
![]()
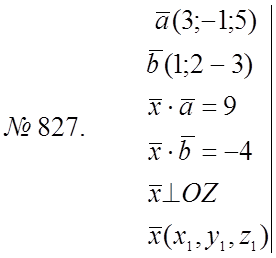
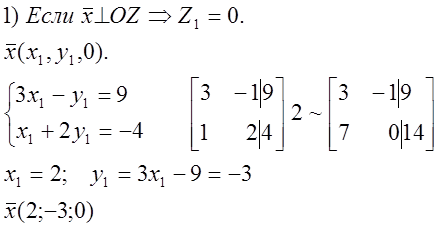
![]() № 826.
№ 826.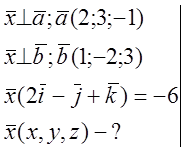
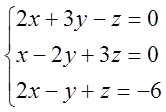
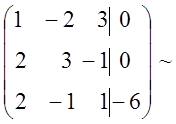
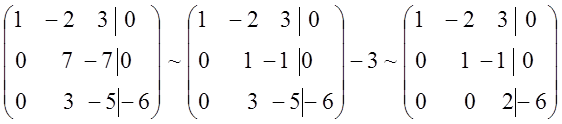
-2z = -6; z = 3; y = z =3; x = 2y –3z =6 – 9 = -3
![]()
Практическое занятие № 9.
1.
Запись: ![]() .
.
2.
Def: Векторным произведением ![]() называется
вектор, обозначаемый
называется
вектор, обозначаемый ![]() и определяемый 3-мя условиями:
и определяемый 3-мя условиями:
1)
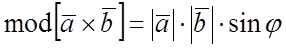 (численно
равен S параллелограмма, построенного на векторах).
(численно
равен S параллелограмма, построенного на векторах).
2)
![]() ^
^![]() и
и ![]() ^
^![]() .
.
3)
![]() направлен
по правилу “правой руки”.
направлен
по правилу “правой руки”.
![]()
![]()
![]()
![]()

![]()
3.
Свойства: 1) ![]() = -
= - ![]() .
.
2) ![]() .
.
3) l × ![]() =
= ![]() .
.
4) ![]() .
.
4.
Если ![]()
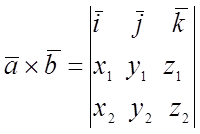
5.
Механический смысл: если ![]() изображает силу,
приложенную к точке М, а
изображает силу,
приложенную к точке М, а
![]() вектор
вектор ![]() , то
, то ![]() , где
, где ![]() - момент силы
- момент силы ![]() относительно
точки О.
относительно
точки О.
b
6.
![]()
 Геометрический смысл:
Геометрический смысл:
S
параллелограмма = ![]()
![]() М a O
М a O
Решение задач.
1), № 850(1,2); 855; 857; 860; 862.
Д. з. № 851; 858; 859; 864.
1) Вычислить S параллелограмма, построенного на векторах
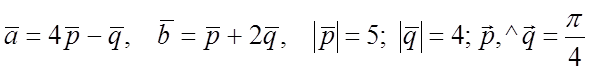
1)![]()
2) Sпар = =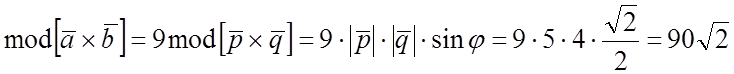
№ 850 (1,2)
![]()
![]()
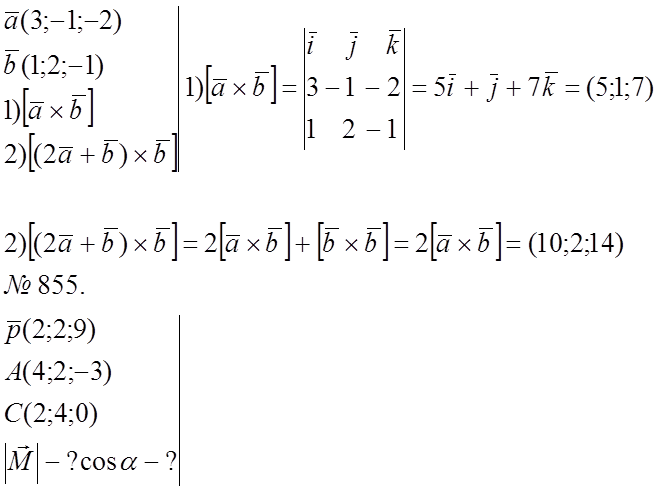

![]() p
p ![]()
![]() А
А
![]() a С
a С
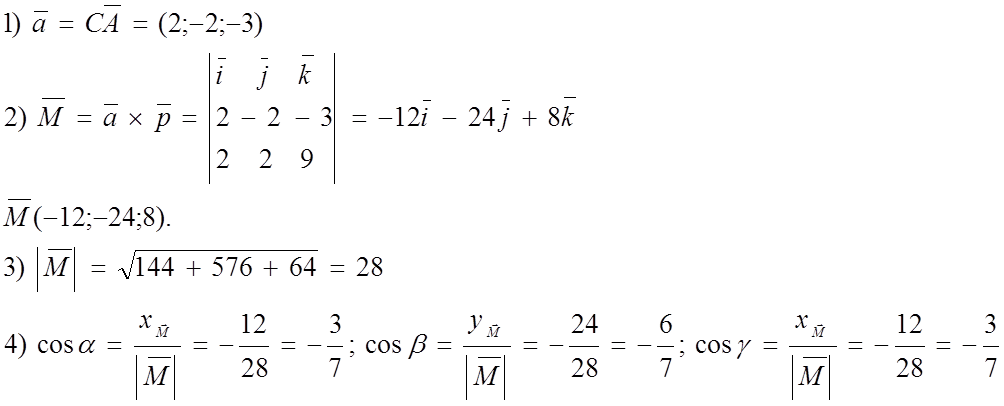
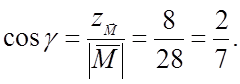
Ответ: 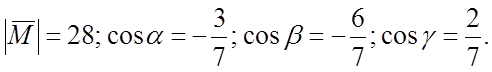
![]()
![]()
 № 857.
№ 857.
B(3;0;-3)
C(5;2;6)
A(1;2;0)
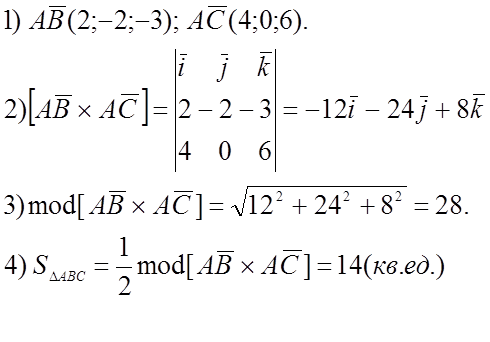
![]() № 860.
№ 860.
![]()
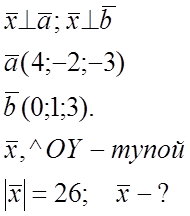 |
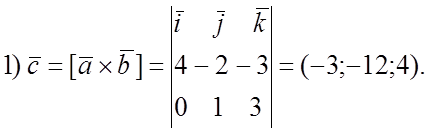
![]()
![]()
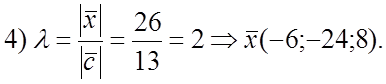
2 Способ. ![]()
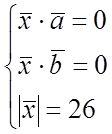
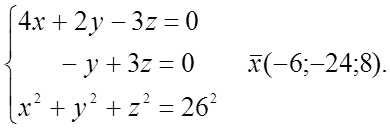
![]() №
862.
№
862.
![]()
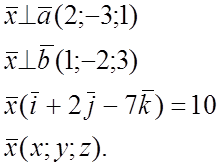
1 СПОСОБ.
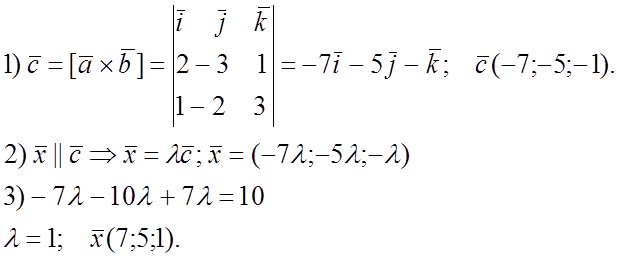
2 СПОСОБ. 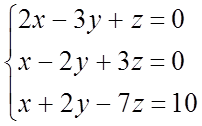
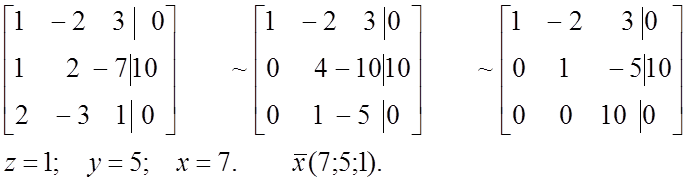
Практическое занятие № 10
Смешанное произведение.
1.
Запись: ![]()
2.
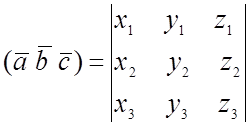
3.
Геометрический смысл: Vпарал
= ![]() .
.
4.
Необходимое и достаточное условие
компланарности 3-х векторов ![]()
5. Не круговая перестановка не меняет величины; перестановка двух соседних сомножителей меняет знак.
Решение задач.
№ 873; 874(1); 875; 876; 877; 867. Д.з. № 866; 869; 878; И. з.
№ 873.
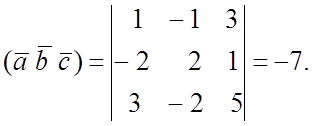
№ 74(1).
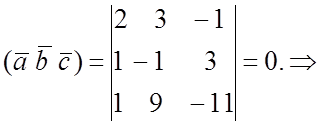 Векторы компланарны (или линейно зависимы).
Векторы компланарны (или линейно зависимы).
№ 875.


![]() B(0;1;5)
B(0;1;5)
C(-1;2;1)
D(2;1;3)
A(1;2;-1)
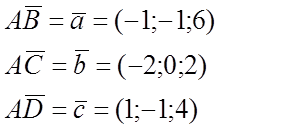
№ 876.
![]()
![]()

![]()
![]()

 D(4;1;3) 1) AB = (3;6;3)
D(4;1;3) 1) AB = (3;6;3)
![]() AC = (1;3;-2)
AC = (1;3;-2)
![]() AD = (2;2;2)
AD = (2;2;2)
B(5;5;4)
A(2;-1;l) C(3;2;-1)
2)
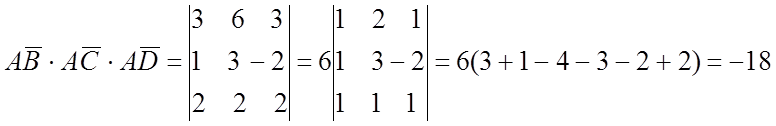
3)
Vтетр = 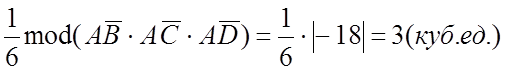
№ 877.
![]()


![]()
![]()

 D
D
A B
C
1)
![]() AB = (2;-2;-3)
AB = (2;-2;-3)
![]() AC = (4;0;6)
AC = (4;0;6)
![]() AD(-7;-7;-7)
AD(-7;-7;-7)
2)
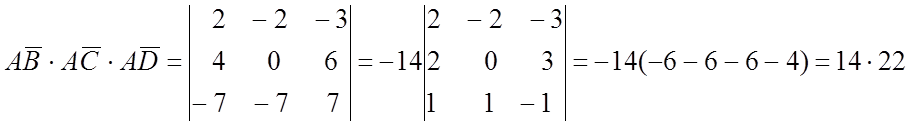 3)
VABCD =
3)
VABCD = 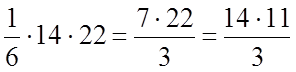
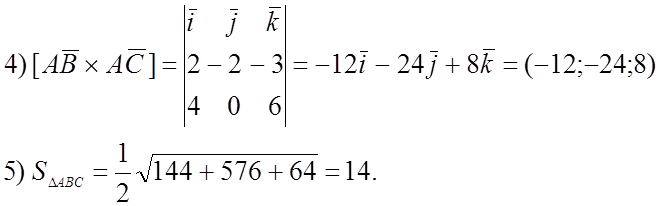
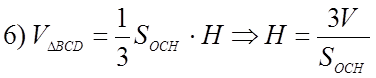
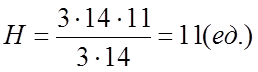 Ответ: 11.
Ответ: 11.
№ 867.
![]()
![]()
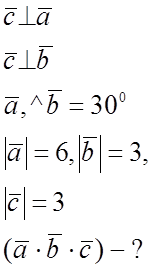
1)
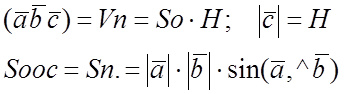
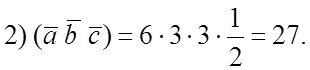
т.к. неизвестно,
левую или правуб тройку образуют векторы, то ![]() .
.
(минус будет, если тройка векторов левая).
Ответ: ![]() .
.
Практическое занятие № 11. Прямая на плоскости.
![]() 1)
1) ![]()
На прямой взяты точки ![]() .
.
![]()
Ax + By + C = 0 – общее уравнение прямой.
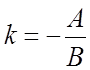 - угловой
коэффициент.
- угловой
коэффициент.
![]()
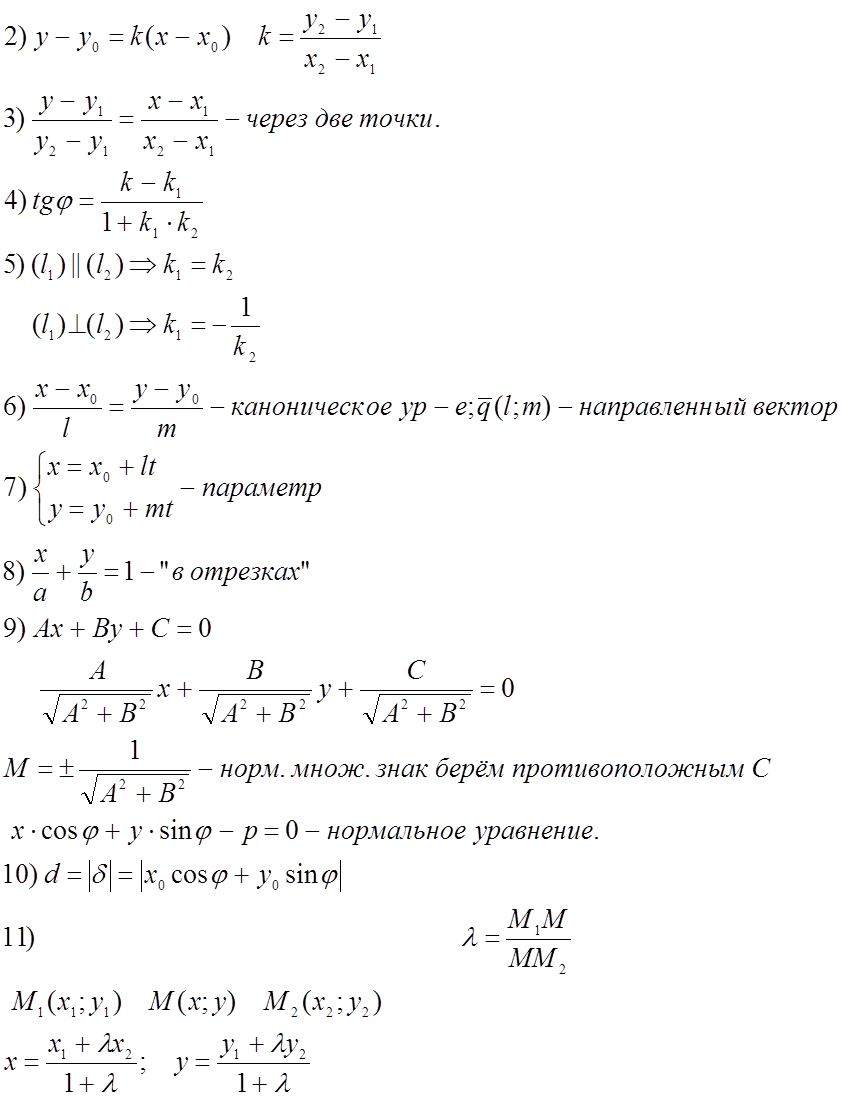
12. Уравнение пучка прямых:
![]()
Решение задач.
№ 218, 226, 234(1), 254, 305(схема), 314, 351.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.