Лінійні диференціальні рівняння, рівняння Бернуллі: Практичне заняття № 2

Практичне заняття №2.

“Лінійні диференціальні рівняння, рівняння Бернуллі”

I. Лінійні диференціальні рівняння

Загальний вигляд лінійних рівнянь першого порядку:

,                               (1)

де Р(х) і Q(х) – задані безперервні функції від х (або постійні).

Рішення рівняння шукаємо у вигляді , , запишемо:

,

групуємо 2-й і 3-й члени, виносячи загальний множник:

.                               (2)

Виберемо функцію v так, щоб вираз в дужках дорівнював нулеві:

        або      .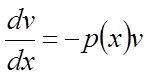

В отриманому рівнянні розділяємо перемінні, помноживши на dx і розділивши обидві частини на v:           .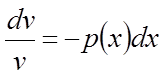

Беремо інтеграл: 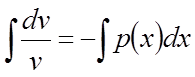, одержимо:

,

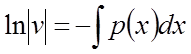звідки 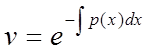         .                                                                                         (3)

Постійну інтегрування беремо рівною нулеві, тому що досить знати хоча б одну функцію. Знайдене значення v підставляємо в праву частину (2), розв'язуємо диференціальне рівняння першого порядку:

.

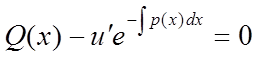Перепишемо останню рівність:

,

,

,               .

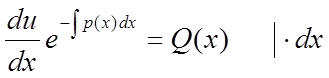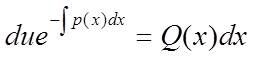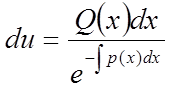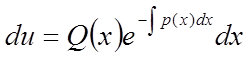Беремо інтеграл від обох частин рівняння:

,

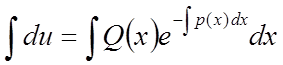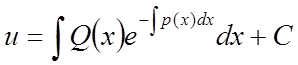.                               (4)

Перемноживши (3) і (4), одержимо загальне рішення рівняння (2):

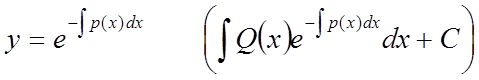                     (5)

Приклад 1.

Розв'язати рівняння: .

Рішення.

Переписавши це рівняння у виді (розділивши обидві частини на х²):

                                 

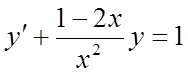
одержимо лінійне рівняння, загальний вид якого:

.

Розв'язуємо це рівняння підстановкою :

.

Підставимо у і у' у рівняння :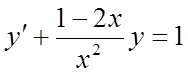

.

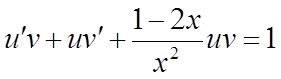Згрупуємо 2-й і 3-й члени рівняння

,

.                               (*)

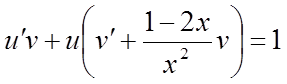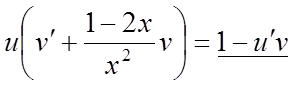Через те, що функції u і v довільні, виберемо їх так, щоб дужка рівняння (*) дорівнювала нулеві:

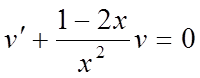            або    ,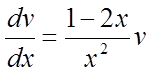

розділимо перемінні, помноживши обидві частини на dx і поділивши на v:

,

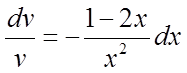беремо інтеграли від обох частин рівняння

.

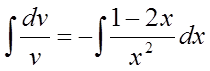
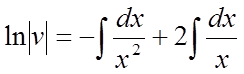
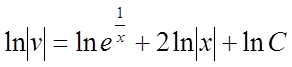
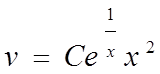Поклавши С = 1, тому що досить знати одну з функцій v, одержимо:

.

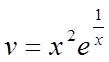Знайдену функцію v підставимо в підкреслену частину рівняння (*) і визначимо другу функцію u:

.

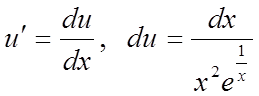
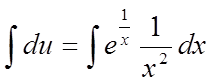Беремо інтеграл, що стоїть в правій частині, за допомогою підстановки:

.

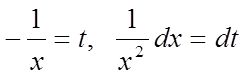Одержимо:

.

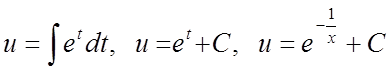Остаточно:

.

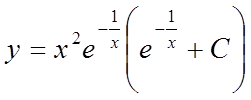Приклад 2.

Розв'язати рівняння: .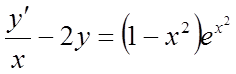

Рішення.

Перепишемо це рівняння у вигляді (помноживши обидві частини на х):

.                                   

Розв'язуємо це рівняння підстановкою ,  .

Підставимо у і у' у рівняння :

.

Згрупуємо 2-й і 3-й члени рівняння

,

.                   (*)

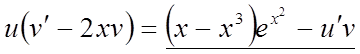Через те, що функції u і v довільні, виберемо їх так, щоб дужка рівняння (*) дорівнювала нулеві:

                    або    ,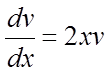

розділимо перемінні, помноживши обидві частини на dx і поділивши на v:

,

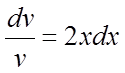беремо інтеграли від обох частин рівняння

,

,

,

.

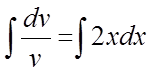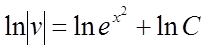
Поклавши С = 1, тому що досить знати одну з функцій v, одержимо:

.

Знайдену функцію v підставимо в підкреслену частину рівняння (*) і визначимо другу функцію u:

         або    .

.

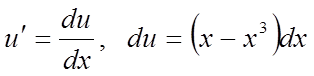
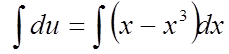Одержимо:

.

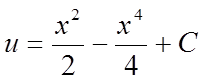Остаточно:

.

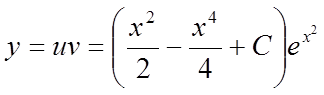II. Рівняння Бернуллі

Рівняння Бернуллі мають вигляд:  (n – число) або . Вирішуються подібно лінійним рівнянням за допомогою підстановки .

Приклад 1.

Розв'язати рівняння: .

Рішення.

Спочатку вирішуємо більш простіший приватний випадок, а саме рівняння

.

Його загальне рішення має вигляд 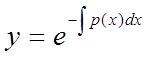. В нашому рівнянні , . Отже, 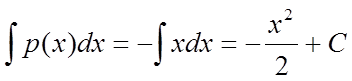,  тому можемо записати:

.

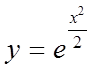Тепер формула перетворення шуканої функції буде

.

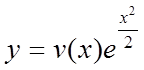Тепер 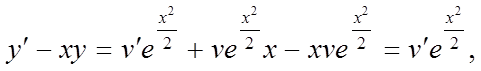 й перетворене рівняння отримає такий вигляд:

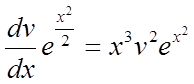   або    .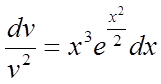

          Інтегруючи, отримаємо

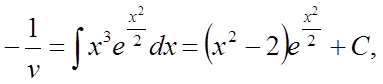
звідки

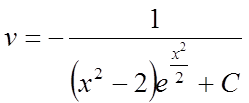
та

,

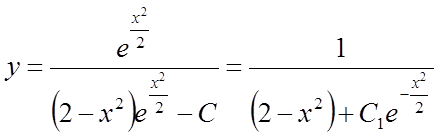де С₁ = С є свавільна постійна.