Лекція 6
План:
1. Метод варіації постійних. Рішення лінійних неоднорідних рівнянь.
2. Лінійні неоднорідні рівняння з постійними коефіцієнтами зі спеціальною правою частиною.
1. Метод варіації постійних. Рішення лінійних неоднорідних рівнянь
Розглянемо тепер лінійне неоднорідне рівняння
![]() . (1)
. (1)
1. Знання
будь-якого приватного рішення рівняння ![]() дозволяє
звести задачу про інтегрування цього рівняння до задачі про інтегрування
відповідного (тобто з відкинутою правою частиною) однорідного рівняння
дозволяє
звести задачу про інтегрування цього рівняння до задачі про інтегрування
відповідного (тобто з відкинутою правою частиною) однорідного рівняння ![]() .
.
Отже, загальне
рішення лінійного неоднорідного рівняння ![]() є сума
будь-якого його приватного рішення та загального рішення відповідного
однорідного рівняння.
є сума
будь-якого його приватного рішення та загального рішення відповідного
однорідного рівняння.
2. Якщо
права частина ![]() дорівнює лінійній комбінації,
наприклад, двох функцій, тобто
дорівнює лінійній комбінації,
наприклад, двох функцій, тобто ![]() , й відомі будь-які
приватні рішення Y1 та Y2 рівняння
, й відомі будь-які
приватні рішення Y1 та Y2 рівняння ![]() з правими частинами
з правими частинами ![]() та
та ![]() , тоді
функція
, тоді
функція
![]()
служить приватним рішенням рівняння ![]() з правою частиною
з правою частиною ![]() .
.
3. Якщо
відомо загальне рішення однорідного рівняння ![]() , то
загальне рішення рівняння
, то
загальне рішення рівняння ![]() можна знайти за допомогою
квадратур.
можна знайти за допомогою
квадратур.
Це робиться за допомогою знайденого Лагранжем методу варіації постійних за наступною схемою.
Як ми знаємо,
загальне рішення рівняння ![]() має вигляд
має вигляд ![]() . Ми шукаємо рішення рівняння
. Ми шукаємо рішення рівняння
![]() у вигляді
у вигляді
![]() , (2)
, (2)
де ![]() – деякі
невідомі поки що функції. Так як їх дві, а рівняння
– деякі
невідомі поки що функції. Так як їх дві, а рівняння ![]() одне,
то для знаходження цих функцій мі накладемо на них ще одне додаткове
співвідношення (4).
одне,
то для знаходження цих функцій мі накладемо на них ще одне додаткове
співвідношення (4).
Диференціюючи рівність (2), отримаємо
![]() . (3)
. (3)
Вимагаємо, щоб друга дужка перевернулась у нуль:
![]() . (4)
. (4)
Тоді при диференціюванні рівності (3) треба приймати до уваги тільки першу дужку, тобто
![]() . (5)
. (5)
Підставляємо усі отримані результати (2), (3), (5) у рівняння (1) не виписуючи нульової суми. Це дасть
![]() .
.
Через те, що
функції у1 та у2 задовольняють рівнянню ![]() , тоді у останньому рівнянні перші дві
дужки відпадають й воно перетворюється у рівність
, тоді у останньому рівнянні перші дві
дужки відпадають й воно перетворюється у рівність
![]() . (6)
. (6)
Отже, для
знаходження у1 та у2 в нас залишились два
співвідношення: (4) та (6). Через те, що у1 та у2
та ![]() вважаються відомими, то отримуємо систему
двох алгебраїчних рівнянь першого ступеню з двома невідомими:
вважаються відомими, то отримуємо систему
двох алгебраїчних рівнянь першого ступеню з двома невідомими: ![]() . Розв'язуючи систему, ми знаходимо ці
невідомі, а інтегруючи, знаходимо у1 та у2.
. Розв'язуючи систему, ми знаходимо ці
невідомі, а інтегруючи, знаходимо у1 та у2.
2. Лінійні неоднорідні рівняння з постійними коефіцієнтами зі спеціальною правою частиною
Приватне рішення ![]() залежить від виду правої частини.
Розглянемо два основні випадки.
залежить від виду правої частини.
Розглянемо два основні випадки.
1. Права
частина рівняння ![]() має вигляд:
має вигляд:
![]() , (7)
, (7)
де ![]() –
багаточлен ступеня n
–
багаточлен ступеня n
![]() .
.
У цьому випадку
приватне рішення ![]() будемо шукати у вигляді:
будемо шукати у вигляді:
![]() , (8)
, (8)
де ![]() –
багаточлен ступеня n з невідомими коефіцієнтами.
–
багаточлен ступеня n з невідомими коефіцієнтами.
Наприклад:
![]()
![]() (9)
(9)
![]()
При цьому
коефіцієнт а показової функції ![]() , що
стоїть в правій частині, не збігається з жодним коренем характеристичного
рівняння.
, що
стоїть в правій частині, не збігається з жодним коренем характеристичного
рівняння.
Якщо коефіцієнт а
збігається з одним коренем характеристичного рівняння, то підібране рішення ![]() (8) варто ще помножити на х; якщо а
збігається з двома коренями характеристичного рівняння, то
(8) варто ще помножити на х; якщо а
збігається з двома коренями характеристичного рівняння, то ![]() помножимо на х2.
помножимо на х2.
Усе сказане можна звести в таблицю
|
Вигляд правої частини |
Корені характеристичного рівняння |
Вигляд приватного рішення |
|
|
1) а ≠ k1 ≠ k2 2) а = k1 ≠ k2 3) а = k1 = k2 |
|
Наприклад: знайти рішення неоднорідного рівняння
![]() .
.
Записуємо відповідне однорідне рівняння
![]() .
.
Складаємо характеристичне рівняння
![]() .
.
Знаходимо його корені:
![]() ,
,
![]() –
дійсні, різні.
–
дійсні, різні.
![]() .
.
Права частина
рівняння ![]() , тобто
, тобто
![]() .
.
Шукаємо приватне рішення у вигляді:
![]() .
.
Визначаємо А.
Диференціюємо ![]() двічі і підставляємо в дане
рівняння:
двічі і підставляємо в дане
рівняння:
![]()
![]()
Остаточно: ![]() .
.
2. Розглянемо другий випадок виду правої частини:
![]() .
.
В окремому випадку може бути:
![]() або
або
![]() , де M і N – відомі числа.
, де M і N – відомі числа.
У кожнім із трьох
можливих випадків приватне рішення ![]() шукається у виді:
шукається у виді:
![]() (10)
(10)
Наприклад:
розв'язати рівняння ![]() .
.
Розв'язуємо
відповідне однорідне рівняння ![]() .
.
Складаємо характеристичне рівняння
![]()
![]() ,
, ![]() ,
, ![]() .
.
Загальне рішення однорідного рівняння запишеться:
![]() .
.
Приватне рішення ![]() підберемо у вигляді:
підберемо у вигляді:
![]() .
.
Диференціюємо двічі і підставляємо в дане рівняння:
![]()
![]()
![]() .
.
Через те, що
отримана рівність є тотожність, вона справедлива, якщо коефіцієнти при ![]() і
і ![]() в
лівій і правій частинах будуть рівними, тобто
в
лівій і правій частинах будуть рівними, тобто
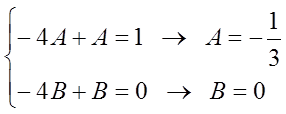
Одержимо
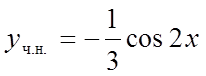 .
.
Остаточно:
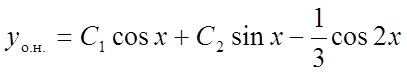 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.