МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
Кафедра «ПРИКЛАДНА МАТЕМАТИКА»
Спеціальність 080202 - «ПРИКЛАДНА МАТЕМАТИКА»
МЕТОДИЧНА ДОКУМЕНТАЦІЯ
з дисципліни «ВИЩА МАТЕМАТИКА ДЛЯ ЕКОНОМІСТІВ (I)»
«Методичні вказівки до практичних
та лабораторних занять »
Луганськ-2004
Практичне заняття № 1.
Тема: Матриці, операції над матрицями. Визначники, їх властивості й обчислення.
Теоретичне
опитування: 1) Визначення матриці розміру ![]() . Види матриць.
. Види матриць.
2) Лінійні операції над матрицями та їх властивості.
3) Операції помноження матриць та їх властивості.
4) Визначник ![]() го порядку. Обчислення визначників 2-го й
3-го
го порядку. Обчислення визначників 2-го й
3-го
порядків.
5) Властивості визначників. Мінор й алгебраїчне доповнення.
6) Обчислення визначників з використанням теореми Лапласу й
приведення до трикутникового вигляду.
7) Зворотна матриця та її обчислення.
Приклади:
1.Знайти
матриці ![]() й обчислити
й обчислити
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3)![]() ; 4)
; 4) ![]() , якщо
, якщо
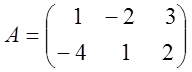 ,
, 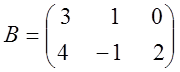 .
.
2.
Обчислити ![]() й
й ![]() та
порівняти їх, якщо
та
порівняти їх, якщо
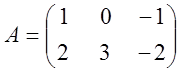 ,
, 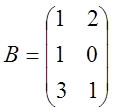 .
.
3. Обчисліть
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() , якщо
, якщо
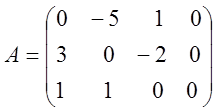 ,
, 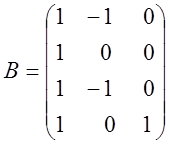 .
.
4. Обчисліть визначники
1) 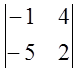 ; 2)
; 2) 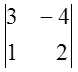 ; 3)
; 3) 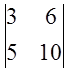 ; 4)
; 4) 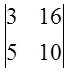 ; 5)
; 5) 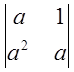 ;
;
6) 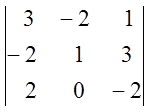 ; 7)
; 7) 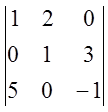 ; 8)
; 8) 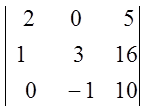 ; 9)
; 9)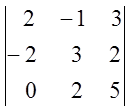 ; 10)
; 10)
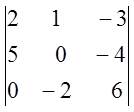 ;
;
11) 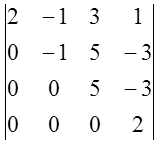 ; 12)
; 12)  ; 13)
; 13)
 ; 14)
; 14) 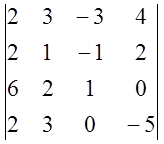 .
.
5. Знайти зворотну матрицю до матриці
1) 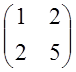 ; 2)
; 2) 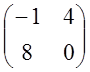 ; 3)
; 3) 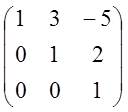 ; 4)
; 4) 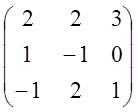 ; 5)
; 5) 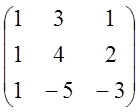 ;
;
6) 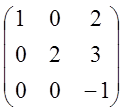 ; 7)
; 7) 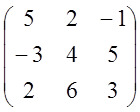 .
.
Домашнє завдання: 1) вивчити теоретичний матеріал: розв’язок матричних рівнянь, методи розв’язку лінійних алгебраїчних систем; 2) розв’язати приклади, які залишились.
]
Практичне заняття № 2.
Тема: Зворотна матриця. Розв’язок матричних рівнянь. Розв’язок лінійних систем рівнянь.
Теоретичне опитування: 1) Ранг матриці та його обчислення.
2)
Як розв’язати матричне рівняння ![]() .
.
3) Визначення системи лінійних алгебраїчних рівнянь.
4) Метод Гаусу розв’язку лінійних систем.
5) Матричний метод розв’язку лінійних систем.
6) Метод Крамеру.
7) Теорема Кронекера-Капеллі.
8) Системи однорідних лінійних рівнянь.
Приклади:
1. Знайти ранг матриць
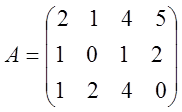 ;
; 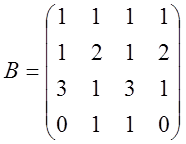 ;
; 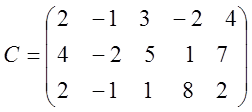 .
.
2. Розв’яжіть матричні рівняння
1) 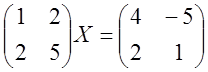 ; 2)
; 2) 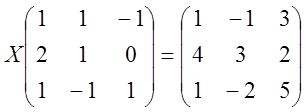 ; 3)
; 3) 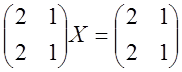 .
.
3. Розв’язати лінійні системи матричним методом
1) 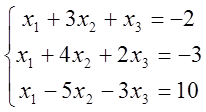 ; 2)
; 2) 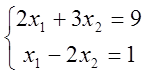 ;
3)
;
3) 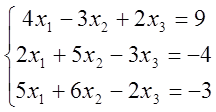 ; 4)
; 4) 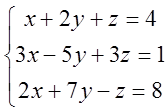 .
.
4. Розв’язати лінійні системи методом Крамеру
1) 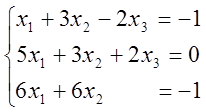 ; 2)
; 2) 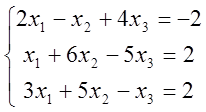 ;
3)
;
3) 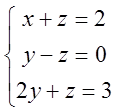 ; 4)
; 4) 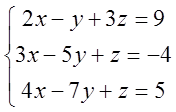 .
.
5. Розв’язати систему методом Гаусу
1) 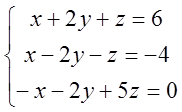 ; 2)
; 2)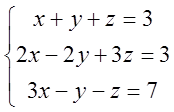 ;
3)
;
3)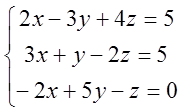 ; 4)
; 4) 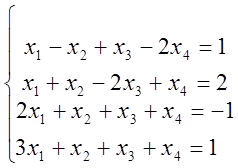 .
.
6. Знайти множину розв’язків однорідної системи
1) 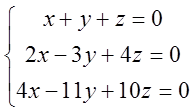 ; 2)
; 2) 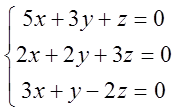 ;
3)
;
3) 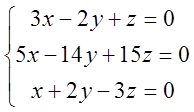 ; 4)
; 4) 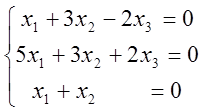 .
.
Домашнє завдання: 1) Вивчити теоретичний матеріал за темою «Вектори»; 2) Розв’язати задачі, які залишились.
Практичне заняття № 3
Тема: Вектори. Операції над векторами.
Теоретичне опитування: 1) Визначення вектору. Модуль. Спрямовуючі косинуси вектору.
2) Лінійні операції над векторами та їх властивості.
3) Скалярний здобуток векторів та його властивості.
4) Векторний здобуток векторів та його властивості.
5) Змішаний здобуток векторів та його властивості.
6)Додаток векторів до розв’язку задач.
7) ![]() мірний векторний простір, розмірність й
базис.
мірний векторний простір, розмірність й
базис.
8) Перехід до нового базису.
9) Евклідовий простір.
![]() ,…,
,…,![]() .
.
Приклади.
а) їх модулі; б) спрямовуючі косинуси; в) їм відповідні одиничні вектори, якщо
1) ![]() ,
, ![]() ; 2)
; 2) ![]() ,
,![]() ; 3)
; 3) ![]() ,
, ![]() .
.
2. Дані вектори ![]() . Знайти координати
векторів
. Знайти координати
векторів ![]() й
й ![]() , якщо
, якщо
![]() ,
,![]() ;
; ![]()
3. Знайти вектор ![]() з рівняння
з рівняння ![]() , якщо
, якщо
![]() ,
, ![]() ,
, ![]() .
.
4. Дані вектори ![]() . Обчислити
. Обчислити ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , якщо
, якщо
![]() ,
, ![]() ;
;![]() ,
, ![]() .
.
5. Дані початок й кінець векторів ![]() й
й ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Знайти координати наступних векторів:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
6. Дані точки ![]() ,
,![]() ,
, ![]() ,
, ![]() .
Встановити чи колінеарні векторів
.
Встановити чи колінеарні векторів ![]() , їх співспрямованість,
відношення модулів.
, їх співспрямованість,
відношення модулів.
7. Визначити, при котрому значенні ![]() вектори
вектори
![]() й
й ![]() взаємно
перпендикулярні.
взаємно
перпендикулярні.
8. Обчислити внутрішні кути трикутнику ![]() ,
, ![]() ,
, ![]() ,
запевнитись, що він рівнобедрений.
,
запевнитись, що він рівнобедрений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.