9) Нескінченно великі функції.
10) зв’язок між нескінченно малими та нескінченно великими функціями.
11) Визначні границі.
12) Обчислення границь.
Відповіді: 1)
2)
3)
4)
5)
Розв’язок задач.
1. Знайти області визначеності функцій
1) 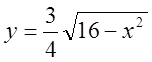 , 2)
, 2) 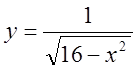 ,
3)
,
3) ![]() , 4)
, 4) ![]() ,
,
5) ![]() , 6)
, 6) ![]() .
.
2. Побудувати графіки елементарних функцій
1) ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
2) ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
3) ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
4) 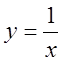 ,
, 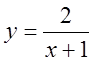 ,
, 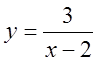 ,
, 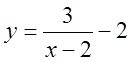 ,
, 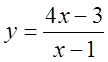 .
.
3. За визначенням границі довести, що:
1) 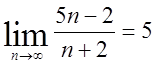 , 2)
, 2) 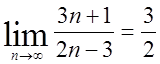 .
.
4. Знайти границі:
1) 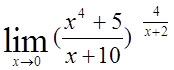 , 2)
, 2) 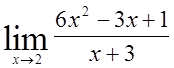 ,
3)
,
3) 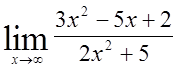 ,
,
4) 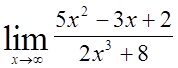 , 5)
, 5) 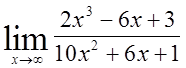 ,
6)
,
6) 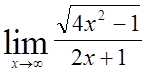 ,
,
7) 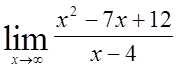 , 8)
, 8) 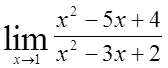 ,
9)
,
9) 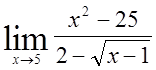 ,
,
10) 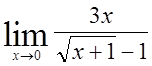 , 11)
, 11) 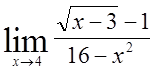 , 12)
, 12) 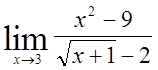 ,
,
13) 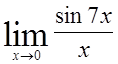 , 14)
, 14) 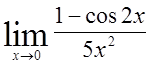 , 15)
, 15) 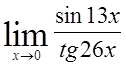 ,
,
16) 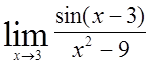 , 17)
, 17) 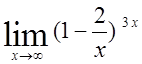 , 18)
, 18) 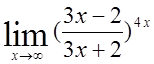 ,
,
19) 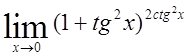 , 20)
, 20) 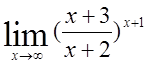 ,
21)
,
21) 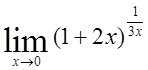 ,
,
22) 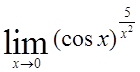 , 23)
, 23) 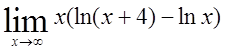 , 24)
, 24) 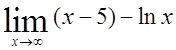 .
.
Домашнє завдання: 1) Вивчити теоретичний матеріал за темою «Неперервність функції. Похідна. Правила диференціювання. Таблиця похідних», 2) розв’язати задачі, які залишились.
Практичне заняття № 6.
Тема: Неперервність функції. Похідна. Правила диференціювання.
Теоретичне опитування: 1) Неперервність функції в точці й області.
2) Властивості функцій неперервних в точці.
3) Властивості функцій неперервних на відрізку.
4) Похідна, її геометричне, фізичне й економічне розуміння.
5) Правила диференціювання. Похідна від важко функції й зворотної функції.
6) Таблиця похідних.
7) Похідні від неявної функції.
Розв’язок задач.
1. Знайти похідні від даних функцій:
1) ![]() , 2)
, 2)![]() , 3)
, 3) ![]() , 4)
, 4) 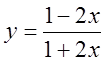 ,
5)
,
5) ![]() ,
,
6) ![]() , 7)
, 7) 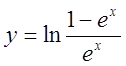 , 8)
, 8)
![]() , 9)
, 9) ![]() ,
,
10) 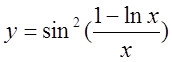 , 11)
, 11) 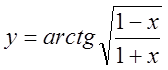 ,
12)
,
12) ![]() ,
,
13) 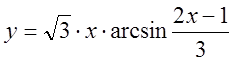 , 14)
, 14) 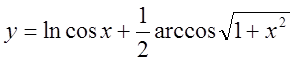 ,
15)
,
15) ![]() .
.
2. Знайти похідні, використовуючи метод логарифмічного диференціювання
1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() , 4)
, 4) 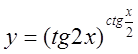 , 5)
, 5) 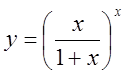 ,
,
6) ![]() .
.
3. Знайти похідні від функцій, щ задані неявно:
1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() , 4)
, 4)![]() ,
,
5) ![]() , 6)
, 6) 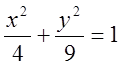 .
.
4. Написати рівняння дотичної ![]() до
графіку функції
до
графіку функції ![]() в точці з абсцисою
в точці з абсцисою ![]() , якщо
, якщо
1) ![]() ,
, ![]() ; 2)
; 2) ![]() ,
, 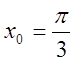 ; 3)
; 3)
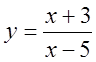 ,
, ![]() .
.
5. Знайти похідні другого порядку від функцій:
1) ![]() , 2)
, 2) 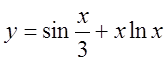 , 3)
, 3)
![]() ,
,
4) ![]() , 5)
, 5) ![]() , 6)
, 6) ![]() .
.
6. Дослідити функцію на неперервність, зробити креслення
1) 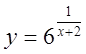 , 2)
, 2) 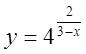 , 3)
, 3) 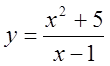 , 4)
, 4) 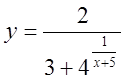 .
.
Домашнє завдання: 1) вивчити теоретичний матеріал за темою «Основні теореми диференціального обчислення. Дослідження функцій за допомогою похідних», 2) розв’язати задачі, які залишились.
Практичне заняття № 7.
Тема: Дослідження функцій за допомогою похідних. Будування графіків функцій.
Теоретичне опитування: 1) Теорема Ферма.
2) Теорема Роллю.
3) Теорема Лагранжу.
4) Правило Лопиталю.
5) Необхідні й достатні умови збільшення функції (зменшення).
6) Визначення екстремуму функції. Необхідна умова екстремуму.
7) Достатня умова екстремуму.
8) Опуклість графіку функції. Необхідна умова опуклості догори (донизу).
9) Точки перетину. Необхідна й достатня умова перетину.
10) Асимптотичні лінії графіку функції: вертикальні, горизонтальні та нахильні.
11)Повна схема дослідження функцій.
Розв’язок задач.
1. Знайти границі, використовуючи правило Лопиталю
1) 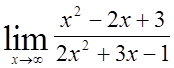 , 2)
, 2) 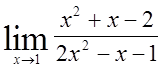 , 3)
, 3)
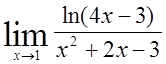 , 4)
, 4) 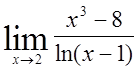 ,
,
5) 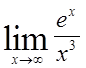 , 6)
, 6) 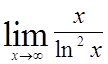 , 7)
, 7) 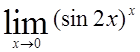 .
.
2. Знайти інтервали монотонності функцій:
1) ![]() , 2)
, 2) ![]() ,
3)
,
3) 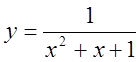 , 4)
, 4) ![]() ,
,
5) 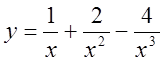 , 6)
, 6) ![]() .
.
3. Знайти екстремум функцій:
1) ![]() , 2)
, 2) ![]() ,
3)
,
3) ![]() ,
,
4) 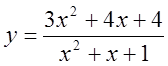 5)
5) ![]() ,
6)
,
6) ![]() ,
,
7) ![]() 8)
8) ![]() ,
9)
,
9) 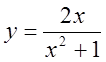 .
.
4. Знайти найбільше й найменше значення функції на вказаних інтервалах:
1) ![]() , 2)
, 2) ![]() ,
,
3) ![]() , 4)
, 4) 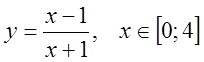 ,
,
5) ![]() , 6)
, 6) 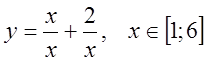 .
.
5. Знайти інтервал опуклості й точки перетину наступних функцій:
1) ![]() , 2)
, 2) ![]() , 3)
, 3) 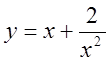 , 4)
, 4) 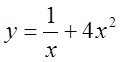 , 5)
, 5) 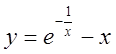 ,
,
6) 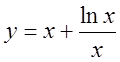 .
.
6. Знайти асимптоти графіків функцій:
1) 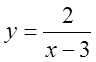 , 2)
, 2) 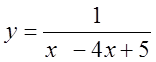 , 3)
, 3) ![]() , 4)
, 4) 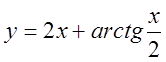 ,
,
5) 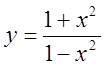 , 6)
, 6) 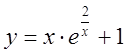 .
.
7. Провести повне дослідження й побудувати графіки наступних функцій:
1) 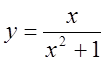 , 2)
, 2) 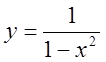 ,
3)
,
3) 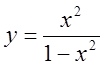 , 4)
, 4) ![]() , 5)
, 5) ![]() ,
,
6) ![]() , 7)
, 7) ![]() , 8)
, 8) 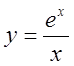 , 9)
, 9) ![]() .
.
Домашнє завдання: 1) підготуватися до контрольної роботи, 2) розв’язати задачі, які залишились.
Практичне заняття № 8.
Тема :підсумкове заняття
1) Проведення контрольної роботи за темою «елементи математичного аналізу».
2) Проведення заліку.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.