9. Дані вершини трикутнику ![]() ,
, ![]() й
й ![]() .
Обчислити довжину його висоти, яка спущена з точці
.
Обчислити довжину його висоти, яка спущена з точці ![]() на
сторону
на
сторону ![]() .
.
10. Встановити, чи компланарні вектори ![]() , якщо
, якщо
1) ![]() ,
, ![]() ,
, ![]() ;
;
2) ![]() ,
, ![]() ,
, ![]() .
.
11. Дані вершини тетраедру ![]() ,
, ![]() ,
, ![]() та
та ![]() . Знайти довжину його висоти, яка спущена з
вершини
. Знайти довжину його висоти, яка спущена з
вершини ![]() .
.
12. Встановити, чи є вектори ![]() лінійно залежними,
якщо:
лінійно залежними,
якщо:
1) ![]() ,
, ![]() ,
, ![]()
2) ![]() ,
, ![]() ,
, ![]() .
.
13. На площині дані дві вершини вектору ![]() ,
, ![]() . Показати, що ці вектори становлять базис
та знайти розклад вектору
. Показати, що ці вектори становлять базис
та знайти розклад вектору ![]() за цим базисом.
за цим базисом.
14. Дані три вектори ![]() ,
, ![]() ,
, ![]() .
Показати, що і вектори становлять базис й знайти розклад вектору
.
Показати, що і вектори становлять базис й знайти розклад вектору ![]() за цим базисом.
за цим базисом.
Домашнє завдання: 1) Вивчити теоретичний матеріал за темою «Пряма на площині. Площина та пряма у просторі»; 2) розв’язати задачі, яки залишились.
Практичне заняття № 4.
Тема: пряма на площині. Площина та пряма у просторі. Проведення контрольної роботи з лінійної алгебри та аналітичної геометрії.
Теоретичне опитування: 1) Метод аналітичної геометрії вивчання властивостей геометричних об’єктів.
2) Види рівнянь прямої на площині
3) Найпростіші задачі на пряму та площу: а) кут між двома прямими; б) умови паралельності та перпендикулярності прямих; в) відстань від точки до прямої.
4) Площина у просторі, загальне рівняння площини.
5) Пряма у просторі й види її рівнянь.
6) Задачі на пряму й площину у просторі.
7) Криві другого порядку та їх класифікація.
8) Еліпс, гіпербола, парабола та їх канонічні рівняння.
аралельною осі Оу.
Приклади
Знайти параметри к й у прямих
1) ![]() , 2)
, 2) ![]() , 3)
, 3)
![]() , 4)
, 4) ![]() .
.
2. Побудувати прямі, котрі задані рівняннями
1) ![]() , 2)
, 2) ![]() ,
3)
,
3) ![]() , 4)
, 4) ![]() , 5)
, 5)
![]() .
.
3. Крізь точку ![]() провести прямі паралельні й
перпендикулярні до прямої
провести прямі паралельні й
перпендикулярні до прямої ![]() :
:
1) ![]() ,
, ![]() ; 2)
; 2) ![]() ,
, ![]() .
.
4. Написати рівняння сторін, висоти й медіан трикутнику з вершинами в
точках ![]() :
:
1) ![]() ,
, ![]() ,
, ![]() , 2)
, 2) ![]() ,
, ![]() ,
, ![]() .
.
5. Знайти точку ![]() перетину бісектрис
внутрішніх кутів трикутнику
перетину бісектрис
внутрішніх кутів трикутнику ![]() , сторони котрого задані
рівняннями:
, сторони котрого задані
рівняннями:
1) ![]() , 2)
, 2) ![]() ,
,
![]() ,
, ![]() ,
,
![]() ;
;
![]() .
.
6. Знайти відстань між паралельними прямими
1) ![]() ,
2)
,
2) ![]() ,
,
![]() ;
;
![]() .
.
7. Даний трикутник з вершинами ![]()
![]() й
й![]() . Знайти рівняння сторін
трикутнику, медіани
. Знайти рівняння сторін
трикутнику, медіани ![]() , висоти
, висоти ![]() та їх довжини.
та їх довжини.
8. Скласти рівняння площини, котра проходить крізь точку ![]() й має нормальний вектор
й має нормальний вектор ![]() .
.
9. Встановити, котрі з наступних пар рівнянь визначають паралельні площини
1) ![]() , 2)
, 2) ![]() ,
3)
,
3) ![]() ,
,
![]() ;
; ![]() ;
; ![]() .
.
10. Скласти рівняння площини, котра проходить крізь точку ![]() паралельно площині
паралельно площині
![]() .
.
11. Довести паралельність прямих 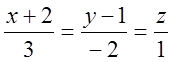 та
та 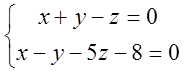 .
.
12. Написати рівняння кола, яке проходить крізь точку ![]() , центр котрої знаходиться в точці
, центр котрої знаходиться в точці
![]() .
.
13. Визначити довжини осів, координати фокусів котрих й ексцентриситет еліпсів задаються рівняннями
1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() .
.
14. Знайти довжини осів, координати фокусів й ексцентриситет гіпербол задаються рівняннями
1) ![]() 2)
2) ![]() 3)
3)
![]() .
.
15. Встановити, що кожне з наступних рівнянь визначає параболу. Знайти
координати її вершини ![]() , величину параметру
, величину параметру ![]() , координати фокусу й рівняння директриси.
, координати фокусу й рівняння директриси.
1) ![]() , 2)
, 2) 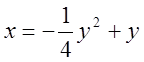 ,
3)
,
3) ![]() .
.
16. Встановити котрі лінії визначаються заданими рівняннями й зробити їх креслення. Знайти координати центру, ексцентриситету й інші їх характеристики
1) 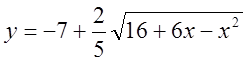 , 2)
, 2) ![]() ,
,
3) 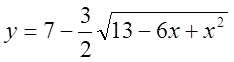 , 4)
, 4) ![]() ,
,
5) ![]() , 6)
, 6)
![]() .
.
Домашнє завдання: 1) вивчити теоретичний матеріал за темою «Функція. Основні поняття. Границя функції. Нескінченно великі й нескінченно малі величини», 2) розв’язати задачі, які залишилися.
Практичне заняття № 5.
Тема: Функція. Основні поняття. Границя функції. Нескінченно великі й нескінченно малі величини.
Теоретичне опитування: 1) Визначення функції. Основні поняття.
2) Основні елементарні функції ті їх графіки.
3) перевтілення графіків функцій.
4) Границя чисельної послідовності.
5)
Границя функції в точці ![]() .
.
6) Визначення нескінченно великої та малої функції.
7) Властивості нескінченно малих функцій.
8) Еквівалентні нескінченно малі функції.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.