Лінійні однорідні рівняння з постійними коефіцієнтами. Теорема про структуру загального рішення лінійного неоднорідного рівняння

Лекція 5

План:

1.  Лінійні однорідні рівняння з постійними коефіцієнтами.

2.  Теорема про структуру загального рішення лінійного неоднорідного рівняння.

1. Лінійні однорідні рівняння другого порядку з постійними коефіцієнтами

Нехай дане лінійне однорідне рівняння другого порядку

,                                (1)

де p і q – постійні дійсні числа. Щоб знайти загальне рішення цього рівняння, досить, як сказано вище, знайти два лінійно незалежні приватні рішення.

Будемо шукати приватне рішення у вигляді , де k – const.

Знайдемо  й  і підставимо в рівняння (1):

,     ,

Через те, що , тому

.                                (2)

Отже, якщо k буде задовольняти рівнянню (2), то  буде рішенням рівняння (1).

Рівняння (2) називається характеристичним рівнянням стосовно рівняння (1). Рівняння (2) має два корені: k₁ і k₂, причому

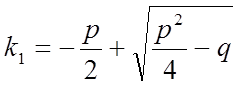       та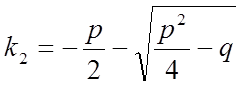      

Можливі випадки:

1)  k₁ і k₂ – дійсні і не рівні між собою числа (k₁ ≠ k₂);

2)  k₁ і k₂ – дійсні рівні числа (k₁ = k₂);

3)  k₁ і k₂ – комплексні числа.

Розглянемо окремо кожен випадок.

Корені характеристичного рівняння дійсні і різні (k₁ ≠ k₂).

У цьому випадку приватними рішеннями будуть функції  і . Покажемо, що ці рішення лінійно незалежні:

.

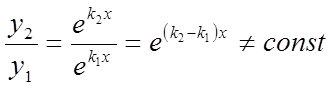Отже, загальне рішення буде мати вигляд

                                        (3)

Корені характеристичного рівняння дійсні і рівні (k₁ = k₂ = k).

Одне приватне рішення будемо шукати у вигляді , а друге – , де u(х) – поки невідома функція.

Диференціюючи у₂ два рази і підставляючи в рівняння (2), визначимо u(х):

, тому що ,

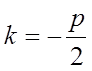, тому що k – кратний корінь характеристичного рівняння.

Отже, щоб знайти u(х), треба вирішити рівняння , через те,  що ; отже .

Інтегруючи останнє два рази, одержимо:

,

де А и В – довільні постійні, котрі можна прийняти: А=1, В=0, тобто маємо .

Таким чином, у якості другого приватного рішення можна вибрати функцію

.

Функції  і   – лінійно незалежні, тому що їхнє відношення не дорівнює const

.

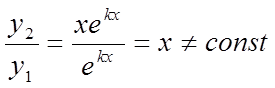Отже, загальне рішення рівняння (2) може бути записане у вигляді

                    (4)

Корені характеристичного рівняння комплексні

Позначимо , .

Приватні рішення рівняння (4) запишемо у вигляді (без доказу):

,              .

Ці функції лінійно незалежні, тому що

,

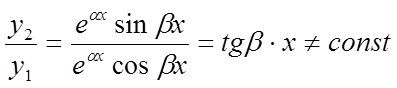і отже, загальне рішення рівняння (2) у цьому випадку запишеться у вигляді:

.                   (5)

Складемо таблицю

№ з/п	Корені характеристичного рівняння	Загальне рішення однорідного рівняння
1	k1 ≠ k2 – різні дійсні
2	k1 = k2 = k – рівні дійсні
3	комплексні

Приклади.

1)       Розв'язати  рівняння .

Складаємо характеристичне рівняння

.

За теоремою Вієта: .

Знаходимо корені

 – корені дійсні, різні.

Загальне рішення згідно (3) запишеться:

2)       Розв'язати рівняння .

Складаємо характеристичне рівняння

.

Знаходимо його корені: .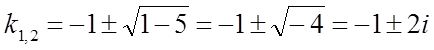

Загальне рішення згідно (5) запишеться:

.

3)       Розв'язати рівняння .

Складаємо характеристичне рівняння

.

Знаходимо його корені: .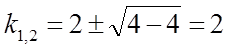

Загальне рішення згідно (4) запишеться:

.

2. Теорема про структуру загального рішення лінійного неоднорідного рівняння

Неоднорідне лінійне рівняння другого порядку має вигляд

                                     (6)

Структура загального рішення такого рівняння визначається наступною теоремою:

Теорема. Загальне рішення неоднорідного представляється як сума загального рішення відповідного однорідного рівняння  і якого-небудь приватного рішення неоднорідного рівняння , тобто

.

Загальне рішення  визначається з вищевикладеного.