Лінійні диференціальні рівняння: однорідні та неоднорідні. Фундаментальна система рішень. Теорема про структуру загального рішення лінійного однорідного рівняння

Лекція 4

План:

1.  Лінійні диференціальні рівняння: однорідні та неоднорідні.

2.   Фундаментальна система рішень.

3.  Теорема про структуру загального рішення лінійного однорідного рівняння.

1. Лінійні диференціальні рівняння: однорідні та неоднорідні

 Визначення 1. Диференціальне рівняння n-го порядку називається лінійним, якщо воно першого ступеня щодо шуканої функції у і її похідних , тобто має вигляд

,                     (1)

де  і  – задані функції від х або постійні.

Якщо 0, то рівняння називається лінійним неоднорідним, якщо , те рівняння називається лінійним однорідним. Перелічимо основні властивості лінійних однорідних рівнянь, обмежуючи рівняннями другого порядку.

1.       Якщо  і  – дві частки рішення лінійного однорідного рівняння другого порядку

                                        (2)

тобто  також рішення цього рівняння.

2.       Якщо  є рішення рівняння (2) і С постійна, тобто  також рішення рівняння (2).

Визначення 2. Два рішення рівняння (2)  і  називаються лінійно незалежними на відрізку , якщо їхнє відношення на цьому відрізку не є постійним, тобто якщо  .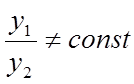

3.       Якщо  і  – два лінійно незалежних рішення рівняння (2), то

,

де  і  – довільні постійні, є його загальне рішення.

2. Фундаментальна система рішень.

Сукупність n лінійно незалежних рішень лінійного однорідного рівняння n-го порядку називають фундаментальною системою рішень. У кожного лінійного однорідного рівняння будь-якого порядку  існує фундаментальна система рішень.

Таким чином, загальне рішення рівняння  – це  лінійна комбінація рішень з фундаментальної системи зі свавільними коефіцієнтами.

3. Теорема про структуру загального рішення лінійного однорідного рівняння.

Будь-яке лінійне однорідне рівняння без правої частини

володіє наступною властивістю: якщо функції у₁ та у₂ є рішеннями рівняння , то й вираз

буде рішенням цього рівняння при усіх значеннях постійних С₁ та С₂.