Линейные операции над векторами, страница 2

Д.з. № 216, 217, 227, 268, 306, 307, 315.

Учить уравнение плоскости в ир – ве.

№ 218.

      С(x₀;y₀).                      

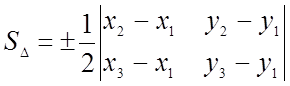
A(1;-2)                        B(2;3)

           

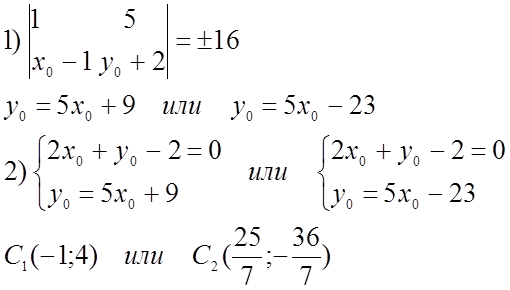
№ 226.

           P(-6;4)

P₁

Прямая имеет уравнение ( l ): 4x - 5y + 3 = 0

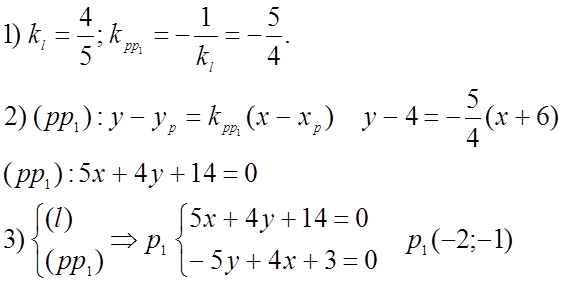
№ 234(1)

                             M₃(3;2)

M₁(2;1)              A             M₂(-1;-1) 

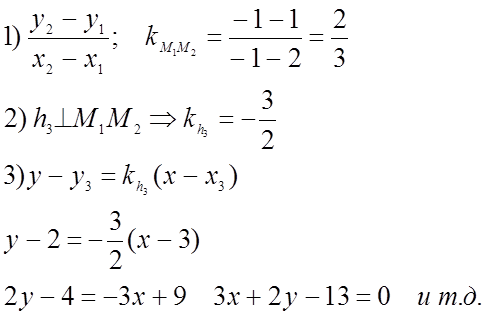
                    M₀(2;1)          

          

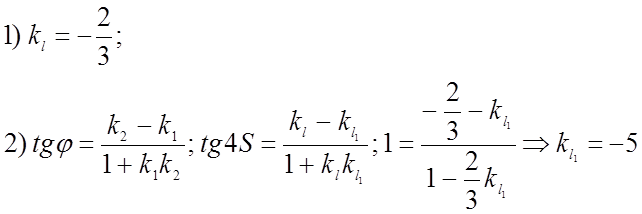
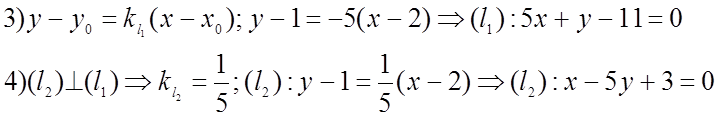
№ 305.

                                         

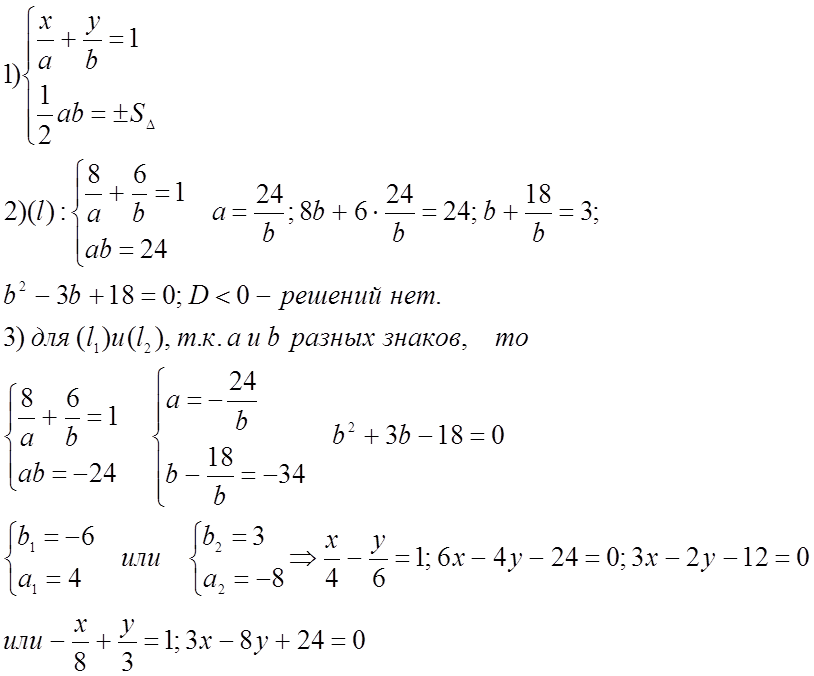
№ 314.

                    A(2;-5)

(l): x - 2y – 7 =0

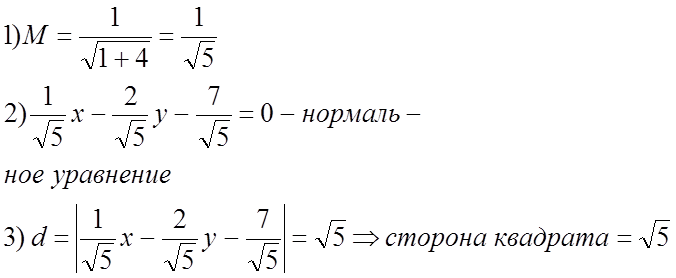
№ 351.

                                    Пусть М(x;y)-текущая точка биссектрисы.

   Т.к. - свободные члены противоположного знака, то для бисектрисы

острого угла берём знак “-”.

Если свободные члены одного знака, то для острого угла берём знак “+”.

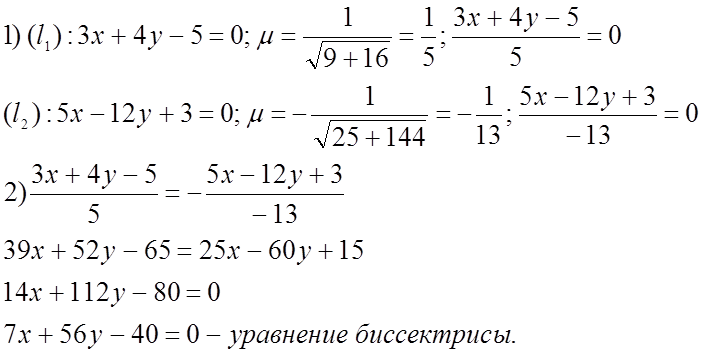
Практическое занятие 12.

Плоскость в пространстве.

1)  - Нормальный вектор.

     

2) 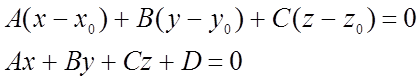 -общее уравнение плоскости в отрезках.

3) 

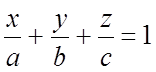
4) 

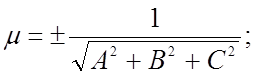
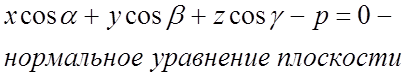
5) 

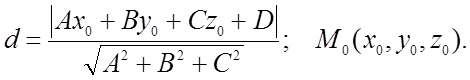
6) 

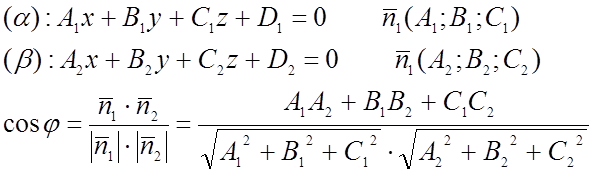
7) 

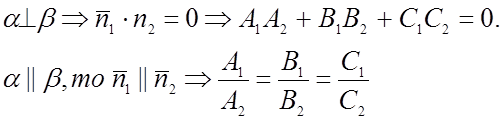
8)  Уравнение плоскости, прохожящей через 3 точки

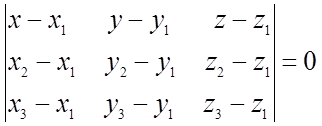
9)  Условие Î 4 точек плоскости:

                                                       Решение задач.

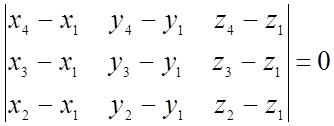№ 917, 928(2), 953, 966, 972(3), 977, 960(сам.)

Д.з. № 919, 926(1), 927(2), 947, 971, 973(1)

№ 917.

На плоскости a взята точка

                

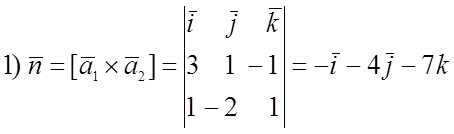
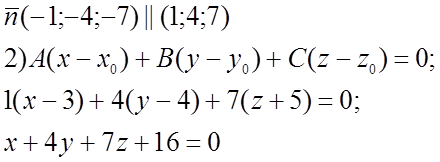
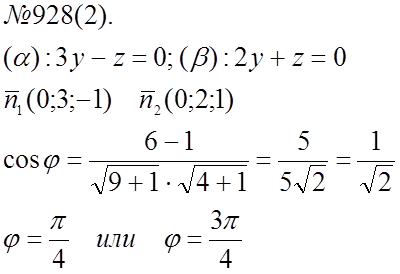
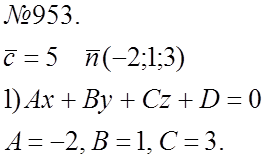
№ 953

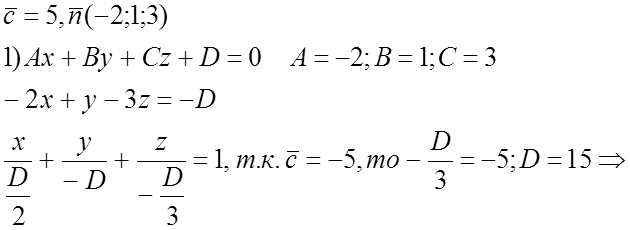
-2x + y +3z +15 = 0 – искомое уравнение.

№ 966.

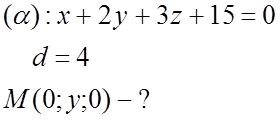
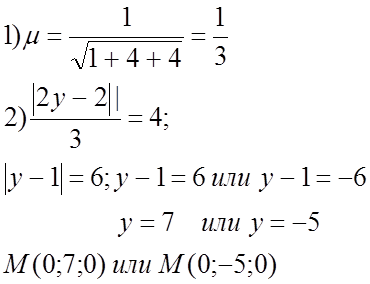
№ 972(3).

                                                                           

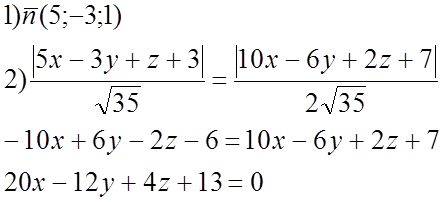
(a):5x-3y+z+3=0

(g)

     

(b): 10x-6y+2z+7=0

№ 977

M(3;2;-1)

(a):5x-y+z+3=0

(b):4x-3y+2z+5=0

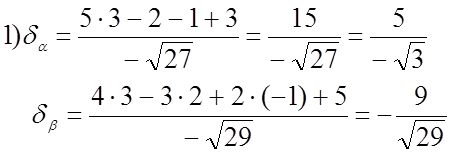
3)  Если d < 0, то т.М и начало координат лежат по одну сторону от плоскости

Т.к. оба отклонения , то угол между плоскостями тупой.

РИСУНОК.

№ 960(самостоятельно).

РИСУНОК.                     

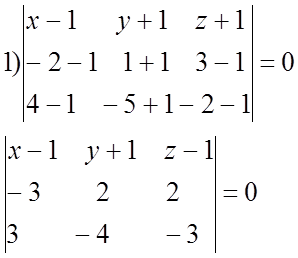
(x-1)×2-(y+1) ×3+(z-1)×6=0

2x – 3y + 6z –11 = 0

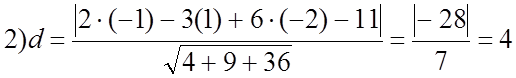
Ответ: d = 4.

Практическое занятие № 13.

Прямая в пространстве.

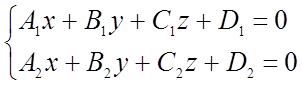         как пересечение двух плоскостей.

2)                                  (l)

                                       

- направляющий вектор.

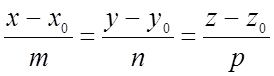- каноническое уравненние прямой.

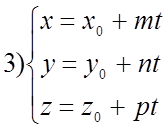- параметрические уравнения прямой

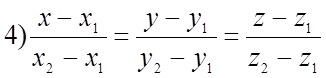 -проходящей через две точки.

                                                  Решение задач.

№ 1011, 1015, 1019(1), 1021(1), 1023, 1026, 1029.

Д.з. 1012, 1018, 1020(1), 1022(2), 1024.

№1011.

                     

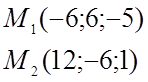
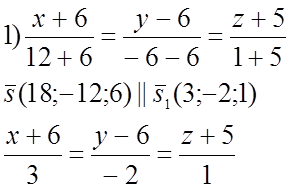
2) Найдём пересечение прямой с пл.OY.

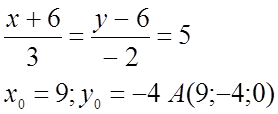
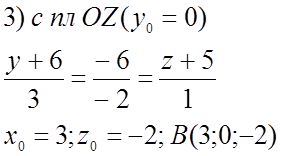
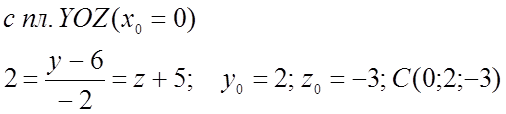
Ответ: (9;-4;0), (3;0;-2), (0;2;-3)

№ 1015

1)  Составим уравнение плоскости(ABC):

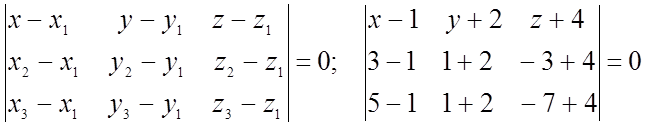
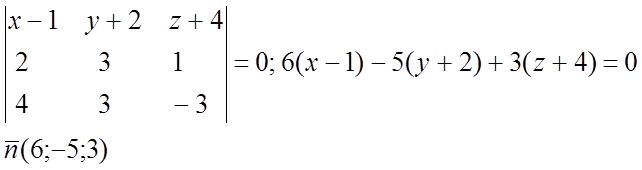
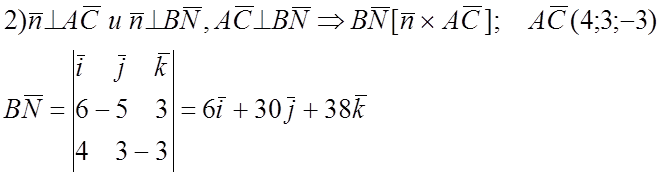
Возьмём коллинеарный ему вектор, кторый будет направляющим вектором высоты BN.    

2)  параметр уравнения выоты BN:

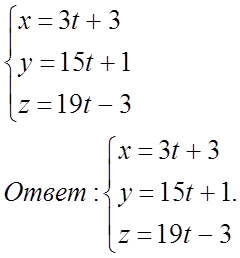
№ 1019. Составить каноническое уравнение прямой.

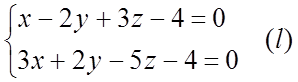
1)  Прямая задана пересечением плоскостей, где

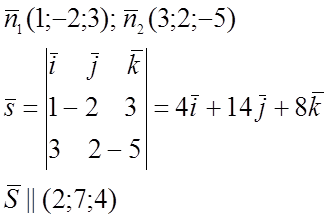
2)  Возьмём произвольную точку

Пусть

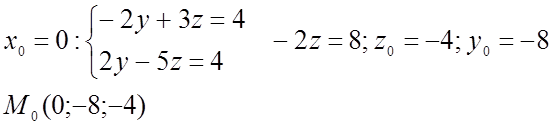
3)  уравнение (l):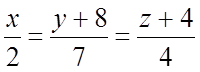

№ 1021(1).

Доказать || прямых

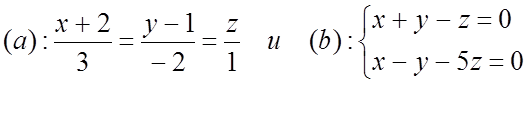
1)  для прямой (а) направленный вектор

2)  для (b) найдём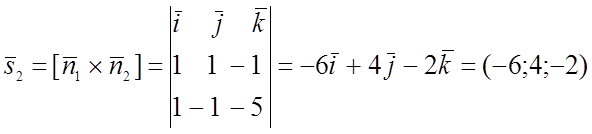

3) 

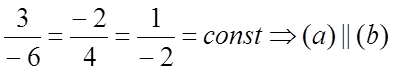
   №1023. Найти острый угол между прямыми.

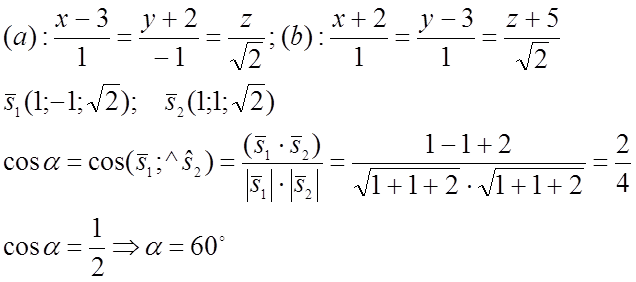
№ 1026. Доказать, что прямые:

           

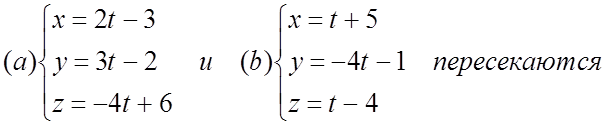
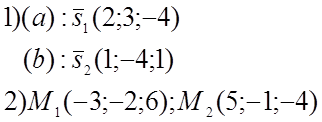
3)Найдём 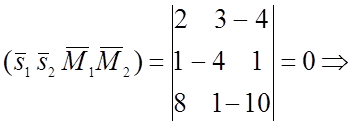три вектора лежат в одной плоскости, т.к. , т.е. прямые (а) и (b) пересекаются.

№1029.

                 

                                

             

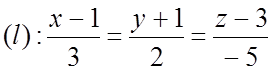
1)  Составим ур-е пл.(a), проходящей через т., нормальный вектор