Линейные операции над векторами, страница 4

№ 193. Вывести уравнение г.м.т., для которых отношение расстояниея до данной точки F(-4;0) к расстоянию до данной прямой 4x + 25 = 0 равно .

                                                        

                                                                              

          Пусть М(x,y)  г.м.т.  

     

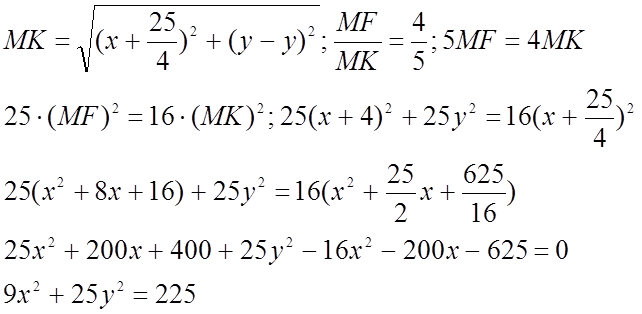
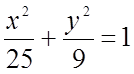 - каноническое уравнение эллипса

№455(2;3)                                                         5

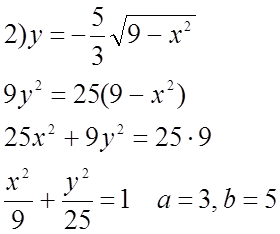                                                     33  3

 

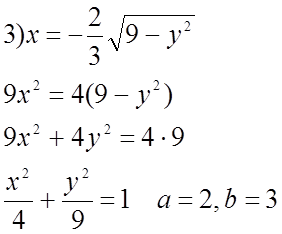
№ 471(1).

 

  

        

      

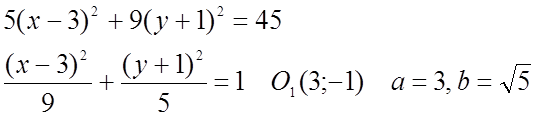
                                                   y                                               

                                                                      y

                                                            x

                                                                                                    x

№ 472(1;3).

 

              

                           

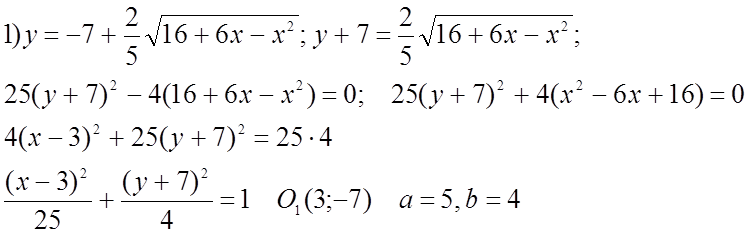
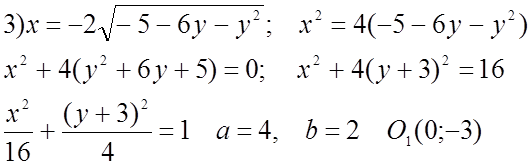
№ 473(1).

                  Решение.

        

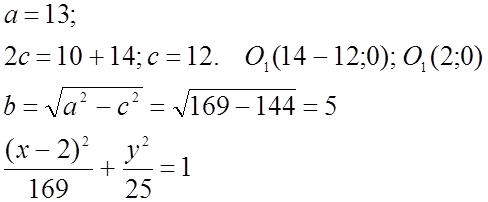
Общая идея :  М(x;y) – текущая точка

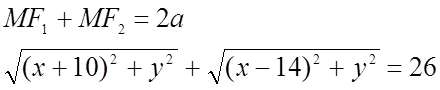       и упрощать.

                                                         ОКРУЖНОСТЬ.

№ 397(5).

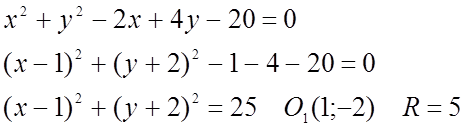
№ 398(3;6).

             

                                                     ГИПЕРБОЛА.

Пусть М(x;y) – текущая точка г.м.т.

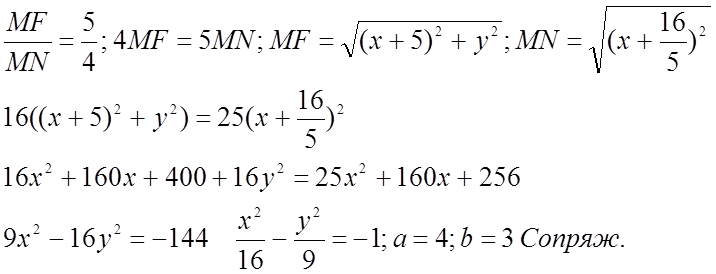
№ 518.

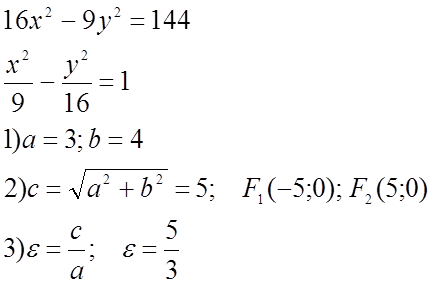
4)Уравнение асимптоты (диагонали основного прямоугольника)

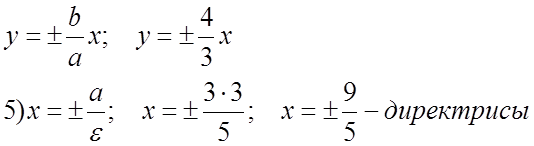
№ 541(1).

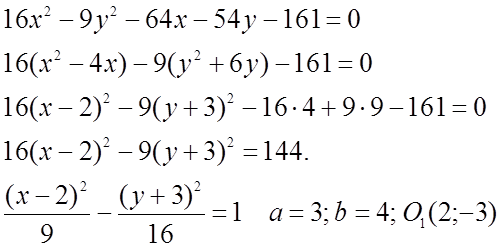
№ 542(3).

   

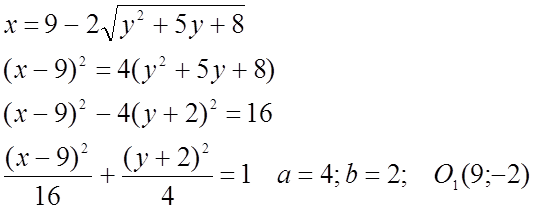
Практическое занятие.

                                                      ПАРАБОЛА

1)  Def: Параболой называется г.м.т., для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстояния до некоторой фиксированной прямой, называемой директрисой.

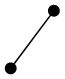
2)                   3)

 MN = MF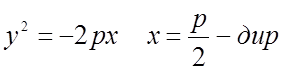                                                       

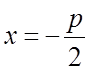- уравнение директрисы.

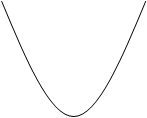
4)                                                                                         

                        5)

                                                     

                                                    Решение задач:

№ 189, 585(1), 588(3;7), 598(2), 599(1;3), 603

Д.з. № 601, 598(3), 599(2;4), 604.

1		ЭЛЛИПС
2		МНИМЫЙ ЭЛЛИПС
3		ТОЧКА
4		ГИПЕРБОЛА(ИЛИ СОПРЯЖ)
5		ПАРА ПЕРЕСЕКАЮЩИХСЯ ПРЯМЫХ
6		ПАРАБОЛА
7		ПАРА || ПРЯМЫХ
8		ПАРА СОВПАДАЮЩИХ ПРЯМЫХ

9

ПАРА МНИМЫХ ПРЯМЫХ

№ 189.

 

Пусть М(x;y)Î г.м.т.    MN = MF

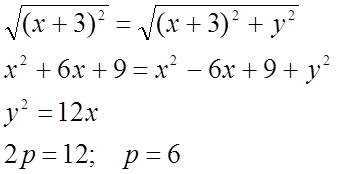
№ 585(1).

А (9;6).  Симметрия относительно  OX.

№ 588(3;7).

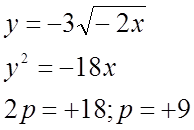3)                                  7)

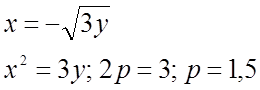
№ 598(2).

                                       

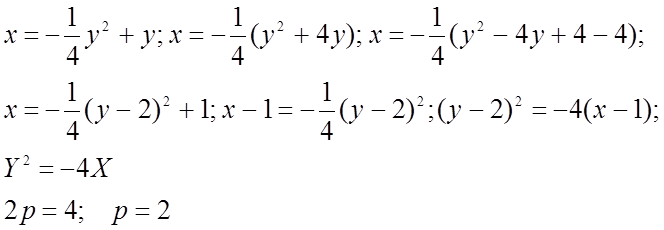
№ 599(1;3)

             

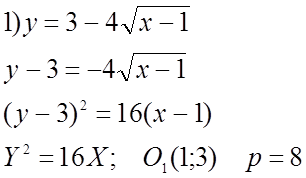
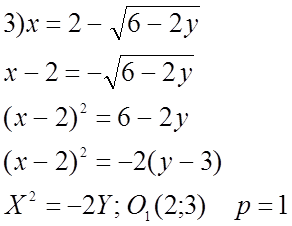
№ 603

          

1)  Найдём проекцию точки А па прямую (l)

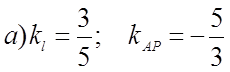
б)составим уравнение (AP): y + 3 = (x - 6)

                                                3y + 9 = -5x + 30

                                                5x + 3y – 21 = 0

в)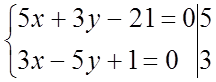   

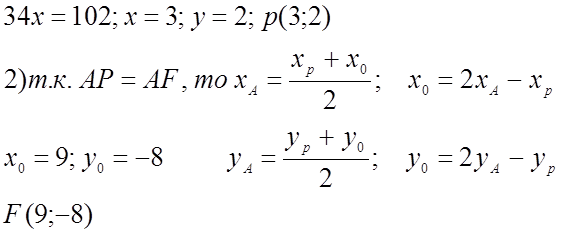
Ответ: F(9;-8).

№ 614.

Составить уравнение прямой, которая касается параболы

                                                 Решение:

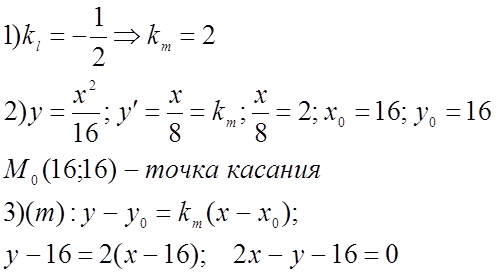
Ответ: .