Криволінійні інтеграли. Умова незалежності інтеграла від лінії інтегрування. Інтегрування повних диференціалів. Первісна функція

Лекція 8

Криволінійні інтеграли (продовження)

 8.1. Умова незалежності інтеграла від лінії інтегрування.

 8.2. Інтегрування повних диференціалів. Первісна функція.

 8.3. Запитання для самоперевірки.

Українсько-російський словник вжитих в лекції слів, які в мовах мають різне звучання.

Винятково – исключительно Обумовленому –                         –оговоренному З’ясувати – выяснить Обстояти – обстоять Допоміжне –                – вспомагательное Відзначити – отметить

Дотримуються –               – придерживаются Цілком – полностью Порушується – нарушается Припущення –                –предположение Протиріччя – противоречие Підсумки – итоги

Первісна – первообразная Доцільний – целесобразный Ланки – звенья Поточна – текущая

Математичні факти з попередніх розділів, які використовуються в даній лекції.

1. Частинні похідні від неперервної в деякій області функції двох змінних  знаходять за тими ж правилами і формулами, що й похідні від функції одної змінної , вважаючи змінною величиною лише ту змінну за якою береться похідна.  Повний диференціал функції дорівньює сумі частинних диференціалів . Аналогічно для функції трьох змінних

2. Для  справедлива теорема про рівність других змішаних похідних:.

3. Ми звикли, що згідно з формулою Ньютона-Лейбніца 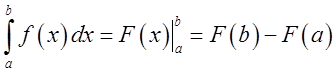 визначений інтеграл є число, але, якщо принаймні одна з границь інтегрування буде змінною величиною  (наприклад верхня границя залежить від t), то результатом інтегрування буде функція  від t .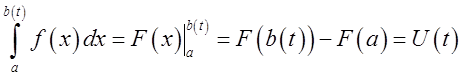

8.1. Умова незалежності інтеграла від лінії інтегрування.

Виникає питання: при яких умовах криволінійний інтеграл (7.2) не залежить від лінії, по якій проходить інтегрування, а залежить винятково від початкової і кінцевої точок лінії інтегрування?

З погляду механіки незалежність інтеграла (7.2) від лінії інтегрування означає, що величина роботи в силовому полі, обумовленому силю  не залежить від форми шляху, а залежить тільки від його початкової і кінцевої точок. Те, що робота в полі земного тяжіння  не залежить від форми шляху, добре відомо з шкільного курсу фізики. Розв’язок  питання, поставленого вище, дозволить з'ясувати, як буде обстояти справа в інших, більш складних, силових полях.

Насамперед доведемо просте допоміжне твердження, що дозволить нам замінити розглянуте питання іншим, рішення якого ми одержимо, спираючись на формулу Гріна.

Лема. Для того щоб криволінійний інтеграл (7.2) не залежав від лінії інтегрування, необхідно і достатньо, щоб цей інтеграл, узятий по будь-якому замкнутому контурі, дорівнював нулю.

Дов-ня. Необхідність  Нехай відомо, що інтеграл (7.2) не залежить від лінії інтегрування; покажемо, що він дорівнює нулю по будь-якому замкнутому контурі. Візьмемо який-небудь замкнутий контур L. Відзначимо на ньому дві точки В и С (рис.8.1.). Так як згідно умови  інтеграл по лінії ВМС дорівнює інтегралу по лінії ВNС: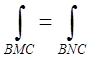,  то інтеграл по всьому контурі L дорівнює .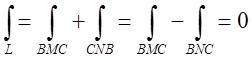

            Достатність. Нехай відомо, що інтеграл (7.2) по всякому замкнутому контуру дорівнює нулю; покажемо, що він не залежить від виду лінії інтегрування.

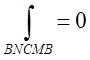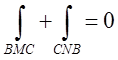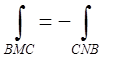. Візьмемо які-небудь дві лінії ВNС і ВМС (рис.8.1), які  з'єднують дві задані точки В и С. Тому, що за умовою інтеграл по замкнутому контурі ВNСМВ дорівнює нулю: ми можемо записати. А звідси легко Рис.8.1             одержимо, що або 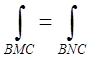і лема повністю доведена.

            Яким же умовам повинна задовільняти підінтегральна функція в (7.2), щоб цей інтеграл не залежав від форми шляху інтегрування. На це питання дає відповідь наступна

Теорема I. Нехай функції неперервні разом зі своїми частинними похідними в однозв'язній області D. Тоді, для того щоб криволінійний інтеграл

(7.2)не залежав від лінії інтегрування, що лежить в області D, необхідно і достатньо, щоб у всіх точках області D,виконувалася рівність

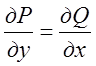
Якщо зазначені властивості функцій Р и О дотримуються при будь-яких х и у, то область D збігається з усією площиною Оху.

Дов-ня. Як було відзначено в лемі, умова незалежності інтеграла від