2.Криволінійний
інтеграл 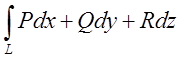 не залежить від лінії інтегрування, що
з'єднує дві дані точки.
не залежить від лінії інтегрування, що
з'єднує дві дані точки.
3.Вираз![]() є повним диференциалом.
є повним диференциалом.
4.В
усіх точках області ![]() має місце рівність
має місце рівність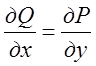 ;
;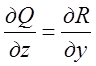 ;
;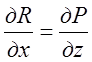 .
.
Останнє твердження буде доведено в лекції 10
після ознайомлення з теоремою Стокса. Це твердження є необхідною умовою того,
щоб вираз ![]() був повним диференціалом, до інтегрування
якого ми і приступимо.
був повним диференціалом, до інтегрування
якого ми і приступимо.
8.2. Інтегрування повних диференціалів. Первісна функція
Будемо розглядати криволінійний інтеграл (7.2),
вважаючи, що виконано всі умови, про які говорилося в попередньому пункті, а
саме; контур L належить
однозв'язній області, у якій функції ![]() і їхні частинні
похідні неперервні, і виконується умова
і їхні частинні
похідні неперервні, і виконується умова 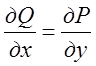 . Тоді величина інтеграла (7.2) залежить винятково від початкової і
кінцевої точок лінії інтегрування і він може записуватися у виді
. Тоді величина інтеграла (7.2) залежить винятково від початкової і
кінцевої точок лінії інтегрування і він може записуватися у виді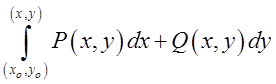 , де
, де ![]() координати
початкової точки лінії інтегрування, а
координати
початкової точки лінії інтегрування, а ![]() –
кінцевої. Який же найбільш доцільний спосіб обчислення такого інтеграла?
Здавалося б, найпростіше інтегрувати по відрізку прямої, який з'єднує дані точки. Однак це не так.
Найраціональніше обчислювати інтеграл вздовж
прямих паралельних координатним осям.
–
кінцевої. Який же найбільш доцільний спосіб обчислення такого інтеграла?
Здавалося б, найпростіше інтегрувати по відрізку прямої, який з'єднує дані точки. Однак це не так.
Найраціональніше обчислювати інтеграл вздовж
прямих паралельних координатним осям.
|
|
Будемо інтегрувати по ламаній ![]() (чи
(чи ![]() ), ланки якої паралельні осям координат
(рис. 8.3)
), ланки якої паралельні осям координат
(рис. 8.3)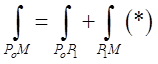 .Обчислимо елементи, які потрібні нам для
переходу до визначеного інтеграла на ділянці
.Обчислимо елементи, які потрібні нам для
переходу до визначеного інтеграла на ділянці ![]() :
: ![]() елементи, які потрібні нам для переходу до
визначеного інтеграла на ділянці
елементи, які потрібні нам для переходу до
визначеного інтеграла на ділянці ![]() :
:
![]() . Підставимо ці значення в (*).
. Підставимо ці значення в (*).
Рис.8.3. 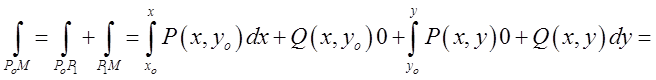
=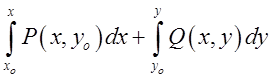 . Аналогічну
формулу одержимо для інтегрування вздовж ламаної
. Аналогічну
формулу одержимо для інтегрування вздовж ламаної ![]() . Якщо
координати верхньої точки є координатами поточної точки, то в результаті такого
інтегрування ми одержимо функцію
. Якщо
координати верхньої точки є координатами поточної точки, то в результаті такого
інтегрування ми одержимо функцію ![]() , повний диференціал
якої і стояв під криволінійним інтегралом. Цю функцію, яку називають первісною,
ми знаходимо з точнівстю до постійної величини С. Якщо ж верхня границя є точка
з конкретними координатами
, повний диференціал
якої і стояв під криволінійним інтегралом. Цю функцію, яку називають первісною,
ми знаходимо з точнівстю до постійної величини С. Якщо ж верхня границя є точка
з конкретними координатами ![]() , то інтеграл буде
дорівнювати приросту первісної
, то інтеграл буде
дорівнювати приросту первісної ![]() тобто
тобто 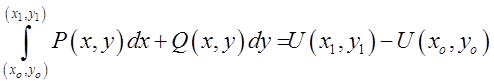 (8.2)
(8.2)
(8.2) називають формулою Ньютона-Лейбніца для криволінійного інтеграла від повного диференціала.
У випадку коли криволінійний інтеграл від повного
диференціала береться по просторовій кривій від точки ![]() до
точки М поступають аналогічно плоскому випадку. Інтеграл знаходять вздовж
ламаної з ланками паралельними координатним осям (рис. 8.4).
до
точки М поступають аналогічно плоскому випадку. Інтеграл знаходять вздовж
ламаної з ланками паралельними координатним осям (рис. 8.4).
|
|
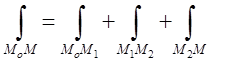 Як і в плоскому випадку запишемо
елементи, які потрібні нам для переходу до визначеного інтеграла на ділянці
Як і в плоскому випадку запишемо
елементи, які потрібні нам для переходу до визначеного інтеграла на ділянці ![]() :
: ![]()
![]() . Елементи, які
потрібні нам для переходу до визначеного інтеграла на ділянці
. Елементи, які
потрібні нам для переходу до визначеного інтеграла на ділянці ![]() :
: ![]()
![]() . Елементи, які
потрібні нам для переходу до визначеного інтеграла на ділянці
. Елементи, які
потрібні нам для переходу до визначеного інтеграла на ділянці ![]() :
: ![]()
![]() . Підставляючи знайдені
величини в три інтеграли, кожен з яких має вид
. Підставляючи знайдені
величини в три інтеграли, кожен з яких має вид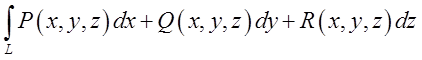 , одержимо
, одержимо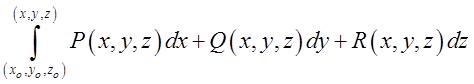 =
=
=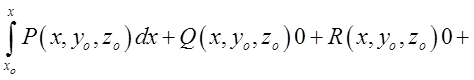
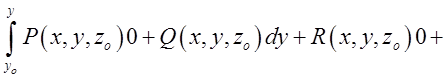
+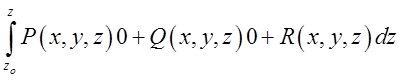 =
=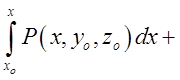
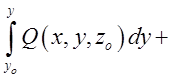
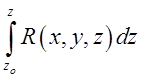 .
.
Формула Ньютона-Лейбніца для криволінійного інтеграла від повного диференціала в трьохвимірному просторі має вид:
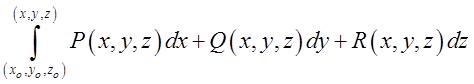 =
=
=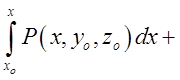
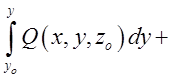
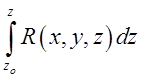 . (8.3)
. (8.3)
Як і плоскому випадку, якщо
верхня границя є точка з конкретними координатами ![]() , то
інтеграл буде дорівнювати приросту первісної, тобто у формулі (8.3) замість
верхніх границь x, y, z треба поставити
, то
інтеграл буде дорівнювати приросту первісної, тобто у формулі (8.3) замість
верхніх границь x, y, z треба поставити ![]() .
.
Запитання для самоперевірки
1. Що означає незалежність криволінійного інтегралу від лінії інтегрування?
2. Показати, що незалежність інтеграла від контуру інтегрування еквівалентне рівності його
нулю по будь-якому замкнутому контурі.
3. Сформулювати і довести теорему про необхідні і достатні умові незалежності
криволінійного інтегралу від лінії інтегрування.
4. Указати, які твердження щодо криволінійного інтегралу і його подінтегрального виразу
еквівалентні в однозв'язній області.
5. Що називається первісної від повного диференціала? Записати формулу Ньютона –
Лейбніца для криволінійних інтегралів.
6. Як визначається криволінійний інтеграл по просторовій лінії?
7. Яка область називається просторово-однозв’язною?
8. Сформулювати теорему про незалежність криволінійного інтегралу від лінії інтегрування
для просторового випадку.
9. Записати формулу Ньютона – Лейбніца для криволінійних інтегралів, заданих по
просторовій кривій.
Розвязати самостійно.
8.1.Обчислити криволінійні інтеграли від повниз диференціалів:
а)
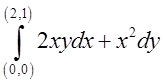 .Відп.
.Відп.![]() б)
б)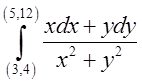 .Відп.
.Відп.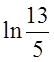 . в)
. в)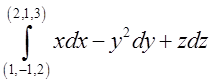 .Відп.
.Відп.![]() .
.
8.2. Знайти функції за заданими повними диференціалами:
а)
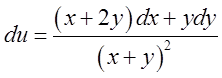 . Відп.
. Відп.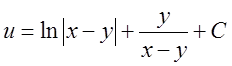 .
.
б)
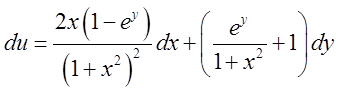 . Відп.
. Відп.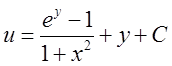 .
.
в)
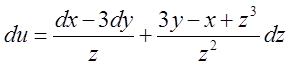 . Відп.
. Відп. 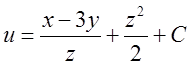 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.